Truss sizing optimisation

This demo showcases how a sizing optimisation of a truss structure can be addressed. For this example we will optimise an inverse truss bridge design.

In particular this demo emphasizes

implementation of a linear elastic truss model with ufl,
creation of (braced) truss meshes, and
the interface to PETSc/TAO for otimisation solvers.

from mpi4py import MPI
from petsc4py import PETSc

import dolfinx
import dolfinx.fem.petsc
import ufl

import matplotlib.pyplot as plt
import matplotlib_inline
import numpy as np
import pyvista as pv

import dolfiny
import dolfiny.taoproblem
from dolfiny.mesh import create_truss_x_braced_mesh

Generation of Truss Meshes¶

Truss structures make up an interesting example of the concept of geometric- and topological dimension, let those be denoted as $d_g$ and $d_t$ , which is also used throughout DOLFINx Baratta et al., 2023.

The geometric dimension is the dimension of the space in which the mesh $\mathcal{T}$ is embedded, $d_g \in \{ 1, 2, 3 \}$ and $\mathcal{T} \subset \mathbb{R}^{d_g}$ , and the topological dimension is the dimension of the cells of the mesh in the reference configuration, $d_t = \dim (\hat{T})$ for $\hat{T}$ the reference cell of $T \in \mathcal{T}$ .

The usual finite element text-book setting applies to the case $d_t = d_g$ , for example a triangle mesh is only considered in $\mathbb{R}^2$ and not in $\mathbb{R}^3$ .

Trusses are made up of lines, or, domain inspecifc, intervals, which are one-dimensional entities $d_t=1$ and form planar or volumetric structures, $d_g \in \{ 2, 3 \}$ . Here, we consider the volumetric case, $d_g=3$ .

The bridge dimensions (length, height, width) are $(100,\, 20,\, 10)$ all in meters and we create the truss mesh from the edges of a (regular) hexahedral mesh, with trusses of size $h=5$ , and introduce all possible bracings to it. This is what the create_truss_x_braced_mesh functionality simplifies. Given a hexehedral mesh, it generates the edge skeleton together with all possible bracings.

comm = MPI.COMM_WORLD
if comm.size > 1:
    raise RuntimeError("Parallelization not supported.")

dim = np.array([100, 20, 10], dtype=np.float64)
elem_size = 5
mesh = create_truss_x_braced_mesh(
    dolfinx.mesh.create_box(
        comm,
        [np.zeros_like(dim), dim],
        (dim / elem_size).astype(np.int32),  # type: ignore
        dolfinx.mesh.CellType.hexahedron,
    )
)

We create one functionspace $V_u = P_1(\mathcal{T})$ for the displacement field $u \in V_u$ and one for the cross sectional area $s$ of the trusses, which we model as constant over each element, so $V_s = DG_0(\mathcal{T})$ .

V_u = dolfinx.fem.functionspace(mesh, ("CG", 1, (3,)))
u = dolfinx.fem.Function(V_u, name="displacement")

V_s = dolfinx.fem.functionspace(mesh, ("DG", 0))
s = dolfinx.fem.Function(V_s, name="cross-sectional-area")

Boundary Conditions and Load Surface¶

For the realisation of an inverse truss bridge, we will fix the trusses on the left and right top edges and apply a vertical load, i.e. in $y$ -direction, on the bridge deck, which we assume to span the whole upper surface/side of the truss mesh, excluding the fixed edges.

mesh.topology.create_connectivity(0, 1)
vertices_fixed = dolfinx.mesh.locate_entities(
    mesh,
    0,
    lambda x: (np.isclose(x[0], 0) | np.isclose(x[0], dim[0])) & np.isclose(x[1], dim[1]),
)

dofs_fixed = dolfinx.fem.locate_dofs_topological(V_u, 0, vertices_fixed)
bcs = [dolfinx.fem.dirichletbc(np.zeros(3, dtype=np.float64), dofs_fixed, V_u)]

vertices_load = dolfinx.mesh.locate_entities(
    mesh, 0, lambda x: np.isclose(x[1], dim[1]) & np.greater(x[0], 0) & np.less(x[0], dim[0])
)
meshtags = dolfinx.mesh.meshtags(mesh, 0, vertices_load, 1)

pv.set_jupyter_backend("static")
pv_grid = pv.UnstructuredGrid(*dolfinx.plot.vtk_mesh(mesh))
plotter = pv.Plotter(window_size=[3840, 2160])
plotter.add_mesh(pv_grid, color="black", line_width=1.5)

for v in vertices_load:
    v_coords = mesh.geometry.x[v]
    arrow = pv.Arrow(start=v_coords + np.array([0, 4, 0]), direction=[0, -1, 0], scale=4)
    plotter.add_mesh(arrow, color="green", opacity=0.5)

for v in vertices_fixed:
    v_coords = mesh.geometry.x[v]
    sphere = pv.Sphere(radius=0.5, center=v_coords)
    plotter.add_mesh(sphere, color="red")

plotter.view_xy()
plotter.add_axes()
plotter.camera.elevation += 20
plotter.camera.zoom(1.7)
plotter.show()

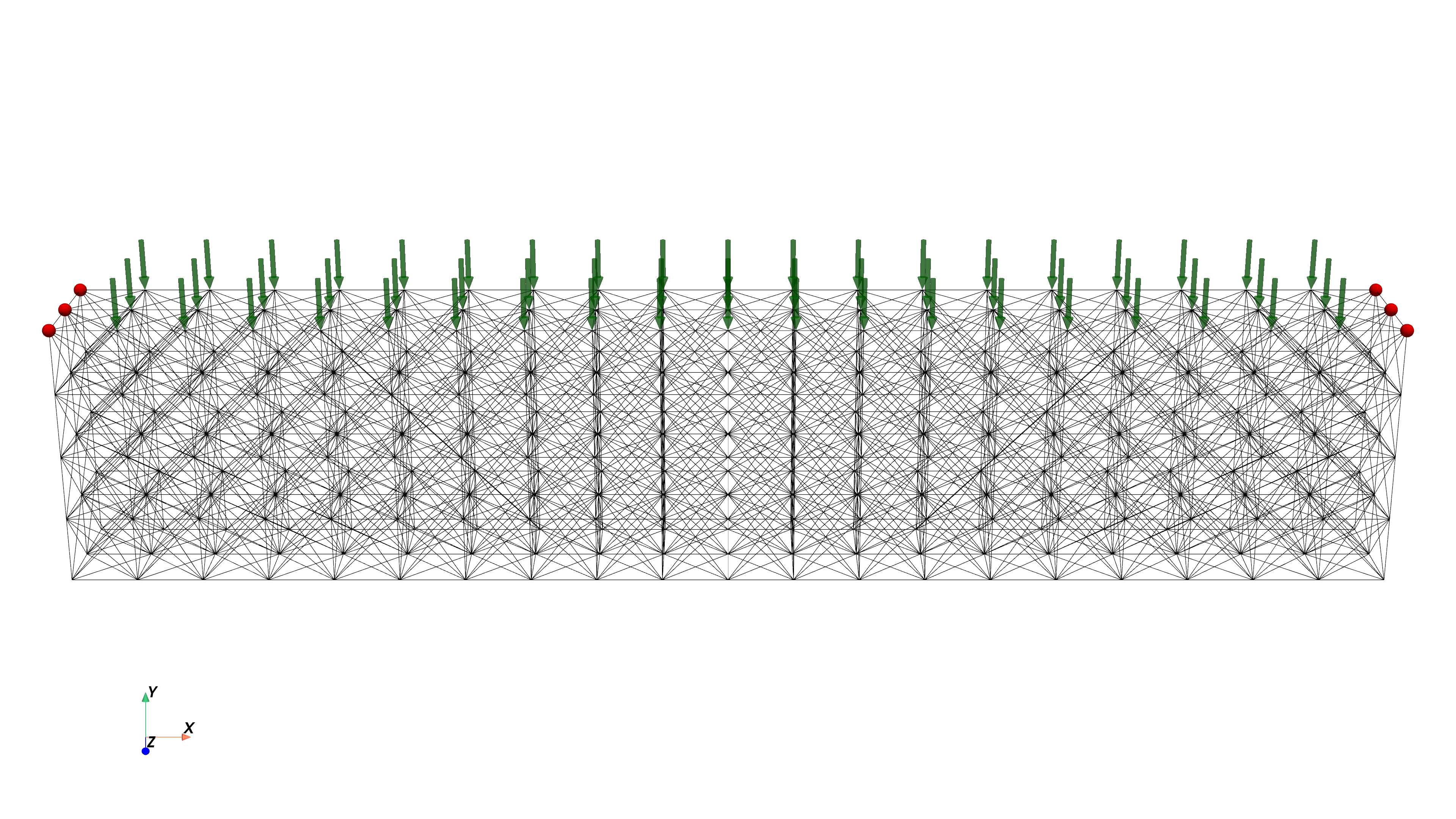
<PIL.Image.Image image mode=RGB size=3840x2160>

Truss Model and Forward Problem¶

We rely on a linear elastic truss model, same as the one presented in Bleyer, 2024. We choose a Young’s modulus of $E = 200\, \text{GPa}$ and apply a total load of $300\, \text{kN}$ , equally distributed across the loaded nodes.

tangent = ufl.Jacobian(mesh)[:, 0]
tangent /= ufl.sqrt(ufl.inner(tangent, tangent))

E = 200.0 * 1e9  # [E] = Pa = N/m^2
ε = ufl.dot(ufl.dot(ufl.grad(u), tangent), tangent)  # strain
N = E * s * ε  # normal_force

dP = ufl.Measure("dP", domain=mesh, subdomain_data=meshtags)
total_load = 300 * 1e3
F = ufl.as_vector([0, -total_load / vertices_load.size, 0])
compliance = ufl.inner(F, u) * dP(1)

E = 1 / 2 * ufl.inner(N, ε) * ufl.dx - compliance

a = ufl.derivative(ufl.derivative(E, u), u)
L = ufl.derivative(compliance, u)

state_solver = dolfinx.fem.petsc.LinearProblem(
    a,
    L,
    bcs=bcs,
    u=u,
    petsc_options={
        "ksp_type": "preonly",
        "pc_type": "lu",
        "pc_factor_mat_solver_type": "mumps",
        "ksp_error_if_not_converged": "True",
        "mat_mumps_cntl_1": 0.0,
    },
    petsc_options_prefix="state_solver",
)

Optimisation of Cross-sectional Areas¶

The truss sizing optimisation problem from Christensen & Klarbring, 2009 we are interested in is given (in reduced form) by

\min_{s \in V_s} C(u(s)) \quad \text{subject to} \quad s_\text{min} \leq s(x) \leq s_\text{max}, \ \int_\Omega s \, \text{d}x = \frac{1}{20} \int_\Omega s_\text{max} \, \text{d} x

(2)

where $u$ is the unique displacement field associated with a given sizing $s$ .

For the bounds of the truss cross sectional area we consider an upper bound of $s_\text{max} = 10^{-2} \, \text{m}^2$ and set the the lower bound to $s_\text{min} = 10^{-3} s_\text{max}$ .

compliance_form = dolfinx.fem.form(compliance)


@dolfiny.taoproblem.sync_functions([s])
def C(tao, x) -> float:
    state_solver.solve()
    return dolfinx.fem.assemble_scalar(compliance_form)  # type: ignore


# p = -u
p = dolfinx.fem.Function(V_u)
gx = dolfinx.fem.form(ufl.derivative(ufl.derivative(E, u, p), s))


@dolfiny.taoproblem.sync_functions([s])
def JC(tao, x, J):
    state_solver.solve()

    J.zeroEntries()
    p.x.array[:] = -u.x.array

    dolfinx.fem.petsc.assemble_vector(J, gx)


s_max = np.float64(1e-2)
s_min = np.float64(1e-3 * s_max)
max_vol = dolfinx.fem.assemble_scalar(dolfinx.fem.form(dolfinx.fem.Constant(mesh, s_max) * ufl.dx))
volume_fraction = 1 / 20
h = [s / max_vol / volume_fraction * ufl.dx <= 1]
s.x.array[:] = 1 / 100 * s_max

opts = PETSc.Options("truss")  # type: ignore
opts["tao_type"] = "python"
opts["tao_python_type"] = "dolfiny.mma.MMA"
opts["tao_monitor"] = ""
opts["tao_max_it"] = (max_it := 50)
opts["tao_mma_move_limit"] = 0.05
opts["tao_mma_subsolver_tao_max_it"] = 30

problem = dolfiny.taoproblem.TAOProblem(
    C, [s], bcs=bcs, J=(JC, s.x.petsc_vec.copy()), h=h, lb=s_min, ub=s_max, prefix="truss"
)


def monitor(tao, comp, volume):
    it = tao.getIterationNumber()
    comp[it] = tao.getPythonContext().getObjectiveValue()
    volume[it] = dolfinx.fem.assemble_scalar(dolfinx.fem.form(h[0].lhs))


comp = np.zeros(max_it, np.float64)
volume = np.zeros(max_it, np.float64)

problem.tao.setMonitor(monitor, (comp, volume))
problem.solve()

state_solver.solve()

  Iteration information for truss solve.
  0 TAO,  Function value: 19614.4,  Residual: 0. 
# TAO   0 (ITERATING)

# sub   0 [  2k] |x|=5.117e-03 |J|=1.025e+07 (cross-sectional-area)

# all            |x|=5.117e-03 |J|=1.025e+07 |h|=0.000e+00 |Jh|=0.000e+00 f=1.961e+04

  1 TAO,  Function value: 3315.56,  Residual: 0. 
# TAO   1 (ITERATING)

# sub   0 [  2k] |x|=2.680e-02 |J|=2.897e+05 (cross-sectional-area)

# all            |x|=2.680e-02 |J|=2.897e+05 |h|=8.000e-01 |Jh|=3.984e+01 f=3.316e+03

  2 TAO,  Function value: 2142.44,  Residual: 0. 
# TAO   2 (ITERATING)

# sub   0 [  2k] |x|=3.489e-02 |J|=1.214e+05 (cross-sectional-area)

# all            |x|=3.489e-02 |J|=1.214e+05 |h|=8.368e-02 |Jh|=3.984e+01 f=2.142e+03

  3 TAO,  Function value: 1648.92,  Residual: 0. 
# TAO   3 (ITERATING)

# sub   0 [  2k] |x|=3.923e-02 |J|=7.770e+04 (cross-sectional-area)

# all            |x|=3.923e-02 |J|=7.770e+04 |h|=6.729e-02 |Jh|=3.984e+01 f=1.649e+03

  4 TAO,  Function value: 1390.03,  Residual: 0. 
# TAO   4 (ITERATING)

# sub   0 [  2k] |x|=4.556e-02 |J|=8.016e+04 (cross-sectional-area)

# all            |x|=4.556e-02 |J|=8.016e+04 |h|=5.449e-02 |Jh|=3.984e+01 f=1.390e+03

  5 TAO,  Function value: 1223.78,  Residual: 0. 
# TAO   5 (ITERATING)

# sub   0 [  2k] |x|=4.995e-02 |J|=4.299e+04 (cross-sectional-area)

# all            |x|=4.995e-02 |J|=4.299e+04 |h|=4.857e-02 |Jh|=3.984e+01 f=1.224e+03

  6 TAO,  Function value: 1109.08,  Residual: 0. 
# TAO   6 (ITERATING)

# sub   0 [  2k] |x|=5.493e-02 |J|=5.084e+04 (cross-sectional-area)

# all            |x|=5.493e-02 |J|=5.084e+04 |h|=4.832e-02 |Jh|=3.984e+01 f=1.109e+03

  7 TAO,  Function value: 1025.34,  Residual: 0. 
# TAO   7 (ITERATING)

# sub   0 [  2k] |x|=5.791e-02 |J|=2.629e+04 (cross-sectional-area)

# all            |x|=5.791e-02 |J|=2.629e+04 |h|=3.917e-02 |Jh|=3.984e+01 f=1.025e+03

  8 TAO,  Function value: 932.513,  Residual: 0. 
# TAO   8 (ITERATING)

# sub   0 [  2k] |x|=6.400e-02 |J|=2.687e+04 (cross-sectional-area)

# all            |x|=6.400e-02 |J|=2.687e+04 |h|=3.706e-02 |Jh|=3.984e+01 f=9.325e+02

  9 TAO,  Function value: 884.561,  Residual: 0. 
# TAO   9 (ITERATING)

# sub   0 [  2k] |x|=6.679e-02 |J|=1.909e+04 (cross-sectional-area)

# all            |x|=6.679e-02 |J|=1.909e+04 |h|=2.624e-02 |Jh|=3.984e+01 f=8.846e+02

 10 TAO,  Function value: 831.9,  Residual: 0. 
# TAO  10 (ITERATING)

# sub   0 [  2k] |x|=7.119e-02 |J|=1.721e+04 (cross-sectional-area)

# all            |x|=7.119e-02 |J|=1.721e+04 |h|=1.803e-02 |Jh|=3.984e+01 f=8.319e+02

 11 TAO,  Function value: 801.734,  Residual: 0. 
# TAO  11 (ITERATING)

# sub   0 [  2k] |x|=7.406e-02 |J|=1.834e+04 (cross-sectional-area)

# all            |x|=7.406e-02 |J|=1.834e+04 |h|=1.140e-02 |Jh|=3.984e+01 f=8.017e+02

 12 TAO,  Function value: 786.914,  Residual: 0. 
# TAO  12 (ITERATING)

# sub   0 [  2k] |x|=7.550e-02 |J|=1.698e+04 (cross-sectional-area)

# all            |x|=7.550e-02 |J|=1.698e+04 |h|=6.276e-03 |Jh|=3.984e+01 f=7.869e+02

 13 TAO,  Function value: 763.783,  Residual: 0. 
# TAO  13 (ITERATING)

# sub   0 [  2k] |x|=7.800e-02 |J|=1.560e+04 (cross-sectional-area)

# all            |x|=7.800e-02 |J|=1.560e+04 |h|=7.674e-03 |Jh|=3.984e+01 f=7.638e+02

 14 TAO,  Function value: 748.808,  Residual: 0. 
# TAO  14 (ITERATING)

# sub   0 [  2k] |x|=8.042e-02 |J|=2.733e+04 (cross-sectional-area)

# all            |x|=8.042e-02 |J|=2.733e+04 |h|=7.190e-03 |Jh|=3.984e+01 f=7.488e+02

 15 TAO,  Function value: 751.909,  Residual: 0. 
# TAO  15 (ITERATING)

# sub   0 [  2k] |x|=7.972e-02 |J|=1.695e+04 (cross-sectional-area)

# all            |x|=7.972e-02 |J|=1.695e+04 |h|=5.554e-03 |Jh|=3.984e+01 f=7.519e+02

 16 TAO,  Function value: 726.702,  Residual: 0. 
# TAO  16 (ITERATING)

# sub   0 [  2k] |x|=8.286e-02 |J|=1.616e+04 (cross-sectional-area)

# all            |x|=8.286e-02 |J|=1.616e+04 |h|=1.256e-02 |Jh|=3.984e+01 f=7.267e+02

 17 TAO,  Function value: 713.137,  Residual: 0. 
# TAO  17 (ITERATING)

# sub   0 [  2k] |x|=8.459e-02 |J|=1.530e+04 (cross-sectional-area)

# all            |x|=8.459e-02 |J|=1.530e+04 |h|=9.076e-03 |Jh|=3.984e+01 f=7.131e+02

 18 TAO,

  Function value: 702.44,  Residual: 0. 
# TAO  18 (ITERATING)

# sub   0 [  2k] |x|=8.625e-02 |J|=1.531e+04 (cross-sectional-area)

# all            |x|=8.625e-02 |J|=1.531e+04 |h|=6.239e-03 |Jh|=3.984e+01 f=7.024e+02

 19 TAO,

  Function value: 690.009,  Residual: 0. 
# TAO  19 (ITERATING)

# sub   0 [  2k] |x|=8.817e-02 |J|=1.364e+04 (cross-sectional-area)

# all            |x|=8.817e-02 |J|=1.364e+04 |h|=6.252e-03 |Jh|=3.984e+01 f=6.900e+02

 20 TAO,

  Function value: 679.203,  Residual: 0. 
# TAO  20 (ITERATING)

# sub   0 [  2k] |x|=9.017e-02 |J|=1.290e+04 (cross-sectional-area)

# all            |x|=9.017e-02 |J|=1.290e+04 |h|=5.602e-03 |Jh|=3.984e+01 f=6.792e+02

 21 TAO,  Function value: 675.623,  Residual: 0. 
# TAO  21 (ITERATING)

# sub   0 [  2k] |x|=9.085e-02 |J|=1.272e+04 (cross-sectional-area)

# all            |x|=9.085e-02 |J|=1.272e+04 |h|=4.684e-03 |Jh|=3.984e+01 f=6.756e+02

 22 TAO,  Function value: 675.236,  Residual: 0. 
# TAO  22 (ITERATING)

# sub   0 [  2k] |x|=9.095e-02 |J|=1.282e+04 (cross-sectional-area)

# all            |x|=9.095e-02 |J|=1.282e+04 |h|=3.681e-03 |Jh|=3.984e+01 f=6.752e+02

 23 TAO,  Function value: 673.486,  Residual: 0. 
# TAO  23 (ITERATING)

# sub   0 [  2k] |x|=9.136e-02 |J|=1.150e+04 (cross-sectional-area)

# all            |x|=9.136e-02 |J|=1.150e+04 |h|=3.492e-03 |Jh|=3.984e+01 f=6.735e+02

 24 TAO,  Function value: 671.741,  Residual: 0. 
# TAO  24 (ITERATING)

# sub   0 [  2k] |x|=9.168e-02 |J|=1.198e+04 (cross-sectional-area)

# all            |x|=9.168e-02 |J|=1.198e+04 |h|=3.710e-03 |Jh|=3.984e+01 f=6.717e+02

 25 TAO,  Function value: 672.325,  Residual: 0. 
# TAO  25 (ITERATING)

# sub   0 [  2k] |x|=9.173e-02 |J|=1.105e+04 (cross-sectional-area)

# all            |x|=9.173e-02 |J|=1.105e+04 |h|=2.905e-03 |Jh|=3.984e+01 f=6.723e+02

 26 TAO,  Function value: 669.717,  Residual: 0. 
# TAO  26 (ITERATING)

# sub   0 [  2k] |x|=9.207e-02 |J|=1.189e+04 (cross-sectional-area)

# all            |x|=9.207e-02 |J|=1.189e+04 |h|=2.930e-03 |Jh|=3.984e+01 f=6.697e+02

 27 TAO,  Function value: 671.428,  Residual: 0. 
# TAO  27 (ITERATING)

# sub   0 [  2k] |x|=9.192e-02 |J|=1.106e+04 (cross-sectional-area)

# all            |x|=9.192e-02 |J|=1.106e+04 |h|=2.255e-03 |Jh|=3.984e+01 f=6.714e+02

 28 TAO,  Function value: 668.967,  Residual: 0. 
# TAO  28 (ITERATING)

# sub   0 [  2k] |x|=9.232e-02 |J|=1.304e+04 (cross-sectional-area)

# all            |x|=9.232e-02 |J|=1.304e+04 |h|=2.630e-03 |Jh|=3.984e+01 f=6.690e+02

 29 TAO,  Function value: 671.666,  Residual: 0. 
# TAO  29 (ITERATING)

# sub   0 [  2k] |x|=9.202e-02 |J|=1.111e+04 (cross-sectional-area)

# all            |x|=9.202e-02 |J|=1.111e+04 |h|=2.285e-03 |Jh|=3.984e+01 f=6.717e+02

 30 TAO,  Function value: 668.425,  Residual: 0. 
# TAO  30 (ITERATING)

# sub   0 [  2k] |x|=9.251e-02 |J|=1.214e+04 (cross-sectional-area)

# all            |x|=9.251e-02 |J|=1.214e+04 |h|=3.350e-03 |Jh|=3.984e+01 f=6.684e+02

 31 TAO,  Function value: 668.046,  Residual: 0. 
# TAO  31 (ITERATING)

# sub   0 [  2k] |x|=9.254e-02 |J|=1.060e+04 (cross-sectional-area)

# all            |x|=9.254e-02 |J|=1.060e+04 |h|=2.472e-03 |Jh|=3.984e+01 f=6.680e+02

 32 TAO,  Function value: 667.11,  Residual: 0. 
# TAO  32 (ITERATING)

# sub   0 [  2k] |x|=9.270e-02 |J|=1.109e+04 (cross-sectional-area)

# all            |x|=9.270e-02 |J|=1.109e+04 |h|=1.509e-03 |Jh|=3.984e+01 f=6.671e+02

 33 TAO,  Function value: 667.134,  Residual: 0. 
# TAO  33 (ITERATING)

# sub   0 [  2k] |x|=9.270e-02 |J|=1.102e+04 (cross-sectional-area)

# all            |x|=9.270e-02 |J|=1.102e+04 |h|=9.261e-04 |Jh|=3.984e+01 f=6.671e+02

 34 TAO,  Function value: 668.263,  Residual: 0. 
# TAO  34 (ITERATING)

# sub   0 [  2k] |x|=9.261e-02 |J|=1.118e+04 (cross-sectional-area)

# all            |x|=9.261e-02 |J|=1.118e+04 |h|=5.980e-04 |Jh|=3.984e+01 f=6.683e+02

 35 TAO,  Function value: 667.581,  Residual: 0. 
# TAO  35 (ITERATING)

# sub   0 [  2k] |x|=9.269e-02 |J|=1.095e+04 (cross-sectional-area)

# all            |x|=9.269e-02 |J|=1.095e+04 |h|=1.029e-03 |Jh|=3.984e+01 f=6.676e+02

 36 TAO,  Function value: 667.153,  Residual: 0. 
# TAO  36 (ITERATING)

# sub   0 [  2k] |x|=9.275e-02 |J|=1.082e+04 (cross-sectional-area)

# all            |x|=9.275e-02 |J|=1.082e+04 |h|=9.733e-04 |Jh|=3.984e+01 f=6.672e+02

 37 TAO,  Function value: 666.849,  Residual: 0. 
# TAO  37 (ITERATING)

# sub   0 [  2k] |x|=9.281e-02 |J|=1.073e+04 (cross-sectional-area)

# all            |x|=9.281e-02 |J|=1.073e+04 |h|=7.591e-04 |Jh|=3.984e+01 f=6.668e+02

 38 TAO,  Function value: 666.431,  Residual: 0. 
# TAO  38 (ITERATING)

# sub   0 [  2k] |x|=9.288e-02 |J|=1.061e+04 (cross-sectional-area)

# all            |x|=9.288e-02 |J|=1.061e+04 |h|=6.380e-04 |Jh|=3.984e+01 f=6.664e+02

 39 TAO,  Function value: 666.256,  Residual: 0. 
# TAO  39 (ITERATING)

# sub   0 [  2k] |x|=9.292e-02 |J|=1.058e+04 (cross-sectional-area)

# all            |x|=9.292e-02 |J|=1.058e+04 |h|=4.288e-04 |Jh|=3.984e+01 f=6.663e+02

 40 TAO,  Function value: 666.078,  Residual: 0. 
# TAO  40 (ITERATING)

# sub   0 [  2k] |x|=9.295e-02 |J|=1.040e+04 (cross-sectional-area)

# all            |x|=9.295e-02 |J|=1.040e+04 |h|=3.030e-04 |Jh|=3.984e+01 f=6.661e+02

 41 TAO,  Function value: 665.969,  Residual: 0. 
# TAO  41 (ITERATING)

# sub   0 [  2k] |x|=9.296e-02 |J|=1.029e+04 (cross-sectional-area)

# all            |x|=9.296e-02 |J|=1.029e+04 |h|=2.525e-04 |Jh|=3.984e+01 f=6.660e+02

 42 TAO,  Function value: 665.898,  Residual: 0. 
# TAO  42 (ITERATING)

# sub   0 [  2k] |x|=9.298e-02 |J|=1.023e+04 (cross-sectional-area)

# all            |x|=9.298e-02 |J|=1.023e+04 |h|=1.225e-04 |Jh|=3.984e+01 f=6.659e+02

 43 TAO,  Function value: 665.936,  Residual: 0. 
# TAO  43 (ITERATING)

# sub   0 [  2k] |x|=9.301e-02 |J|=1.027e+04 (cross-sectional-area)

# all            |x|=9.301e-02 |J|=1.027e+04 |h|=7.149e-05 |Jh|=3.984e+01 f=6.659e+02

 44 TAO,

  Function value: 666.018,  Residual: 0. 
# TAO  44 (ITERATING)

# sub   0 [  2k] |x|=9.296e-02 |J|=1.020e+04 (cross-sectional-area)

# all            |x|=9.296e-02 |J|=1.020e+04 |h|=6.749e-05 |Jh|=3.984e+01 f=6.660e+02

 45 TAO,  Function value: 665.935,  Residual: 0. 
# TAO  45 (ITERATING)

# sub   0 [  2k] |x|=9.302e-02 |J|=1.025e+04 (cross-sectional-area)

# all            |x|=9.302e-02 |J|=1.025e+04 |h|=2.009e-04 |Jh|=3.984e+01 f=6.659e+02

 46 TAO,  Function value: 665.865,  Residual: 0. 
# TAO  46 (ITERATING)

# sub   0 [  2k] |x|=9.302e-02 |J|=1.023e+04 (cross-sectional-area)

# all            |x|=9.302e-02 |J|=1.023e+04 |h|=1.783e-04 |Jh|=3.984e+01 f=6.659e+02

 47 TAO,  Function value: 665.882,  Residual: 0. 
# TAO  47 (ITERATING)

# sub   0 [  2k] |x|=9.304e-02 |J|=1.035e+04 (cross-sectional-area)

# all            |x|=9.304e-02 |J|=1.035e+04 |h|=9.636e-05 |Jh|=3.984e+01 f=6.659e+02

 48 TAO,  Function value: 665.979,  Residual: 0. 
# TAO  48 (ITERATING)

# sub   0 [  2k] |x|=9.306e-02 |J|=1.032e+04 (cross-sectional-area)

# all            |x|=9.306e-02 |J|=1.032e+04 |h|=9.086e-05 |Jh|=3.984e+01 f=6.660e+02

 49 TAO,  Function value: 665.892,  Residual: 0. 
# TAO  49 (ITERATING)

# sub   0 [  2k] |x|=9.310e-02 |J|=1.033e+04 (cross-sectional-area)

# all            |x|=9.310e-02 |J|=1.033e+04 |h|=2.063e-04 |Jh|=3.984e+01 f=6.659e+02

Coefficient(FunctionSpace(Mesh(blocked element (Basix element (P, interval, 1, gll_warped, unset, False, float64, []), (3,)), 1), blocked element (Basix element (P, interval, 1, gll_warped, unset, False, float64, []), (3,))), 0)

# verify result
# if problem.tao.getConvergedReason() <= 0:
#     raise RuntimeError("Optimisation did not converge.")

if np.abs(dolfinx.fem.assemble_scalar(dolfinx.fem.form(h[0].lhs)) - h[0].rhs) >= 1e-2:
    raise RuntimeError("Volume constraint violated.")

if np.any(s.x.array < s_min):
    raise RuntimeError("Lower bound violated.")

if np.any(s.x.array > s_max):
    raise RuntimeError("Upper bound violated.")

Convergence of the optimisation, that is the compliance and the volume vs. outer MMA iteration are shown below. Compliance is measured relative to the initial compliance $C_0$ , which is compliance for the initial guess of $s_\text{init} = 10^{-2} \, \text{m}^2$ . Volume is shown relative to the upper bound $V_\text{max}$ .

matplotlib_inline.backend_inline.set_matplotlib_formats("png")
it = problem.tao.getIterationNumber()
comp = comp[:it]  # type: ignore
volume = volume[:it]  # type: ignore

fig, ax1 = plt.subplots(dpi=400)
ax1.set_xlim(0, it - 1)
ax1.set_xlabel("Outer MMA iteration")
ax1.set_ylabel("Rel. compliance $C / C_0$")
plt_compliance = ax1.plot(
    np.arange(0, it, dtype=int),
    comp / comp[0],
    color="tab:orange",
    marker="x",
)
ax1.set_yscale("log")
ax1.grid(True, which="both")

ax2 = ax1.twinx()
ax2.set_ylabel(r"$|1 - V / V_\text{max}|$")
plt_volume = ax2.plot(np.arange(0, it, dtype=int), np.abs(1 - volume / h[0].rhs), marker=".")
ax2.axhline(y=1, linestyle="--")
ax2.set_yscale("log")
ax1.legend(plt_compliance + plt_volume, ["compliance", "volume"], loc=7)

plt.show()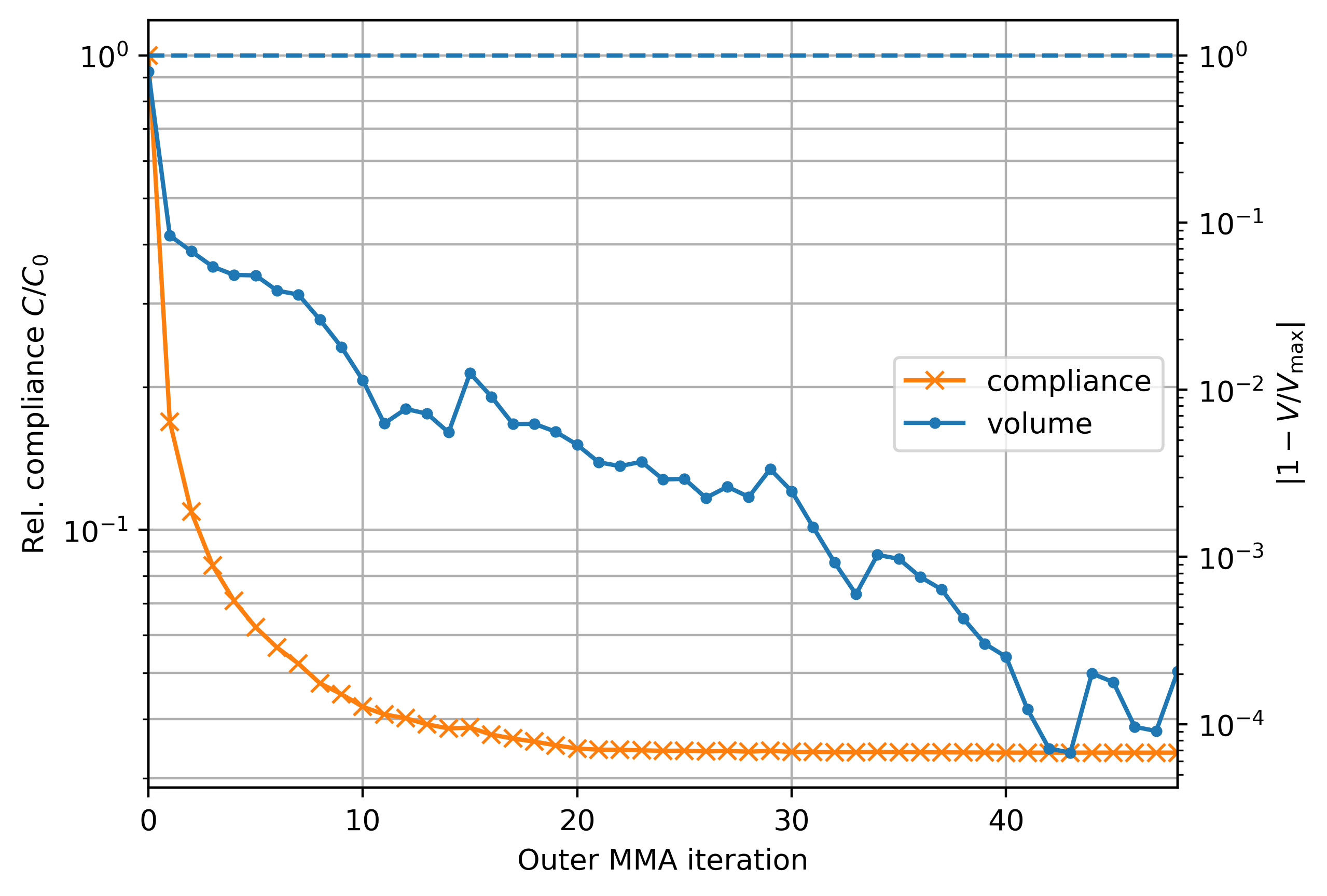

The deformed final design (displacement scaled by $5\times10^3$ )

pixels = dolfiny.pyvista.pixels
plotter = pv.Plotter(window_size=[pixels, pixels // 2])

pv_grid.point_data[u.name] = u.x.array.reshape(-1, 3)
pv_grid.cell_data[s.name] = s.x.array

plotter.add_mesh(pv_grid.warp_by_vector(u.name, factor=5e3), color="black", line_width=1.5)

plotter.add_axes()
plotter.view_xy()
plotter.camera.elevation += 20
plotter.camera.zoom(2.0)
plotter.show()

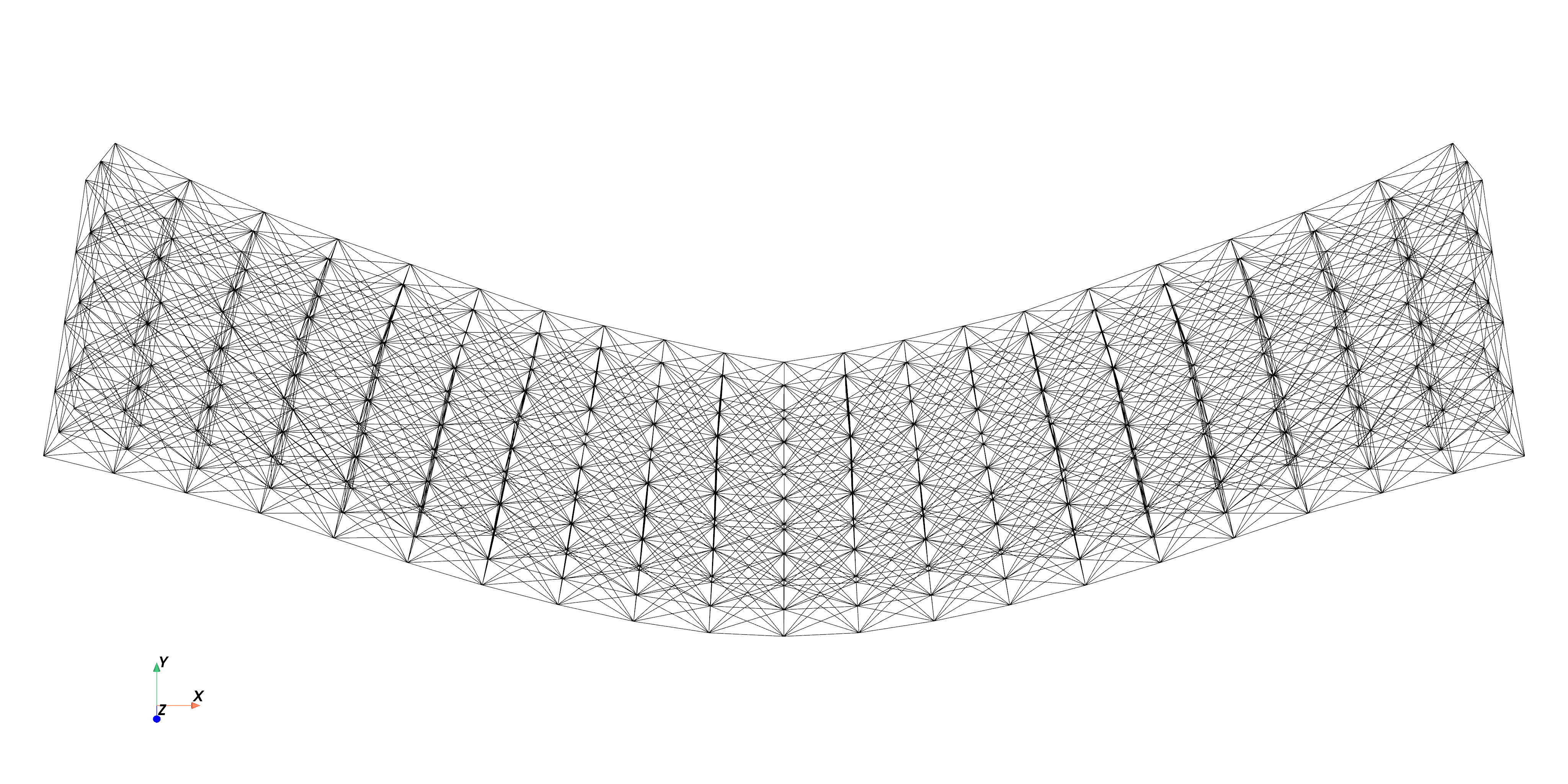
<PIL.Image.Image image mode=RGB size=4096x2048>

Visualisation of the optimised truss structure, each truss plotted corresponding to optimisation result (opacity of tubes according to ratio of maximal allowed cross sectional area). Radii are scaled by factor of 5, for visualisation purposes.

plotter = pv.Plotter(window_size=[pixels, pixels // 2])

radius = np.sqrt(s.x.array / np.pi)
radius_max = np.sqrt(s_max / np.pi)
e_to_v = mesh.topology.connectivity(1, 0)
for e_idx in range(e_to_v.num_nodes):
    a, b = e_to_v.links(e_idx)
    plotter.add_mesh(
        pv.Tube(
            pointa=mesh.geometry.x[a],
            pointb=mesh.geometry.x[b],
            radius=radius[e_idx] * 5,
            capping=True,
        ),
        opacity=radius[e_idx] / radius_max,
    )
plotter.add_axes()
plotter.view_xy()
plotter.camera.elevation += 20
plotter.camera.zoom(2.0)
plotter.show()

References¶

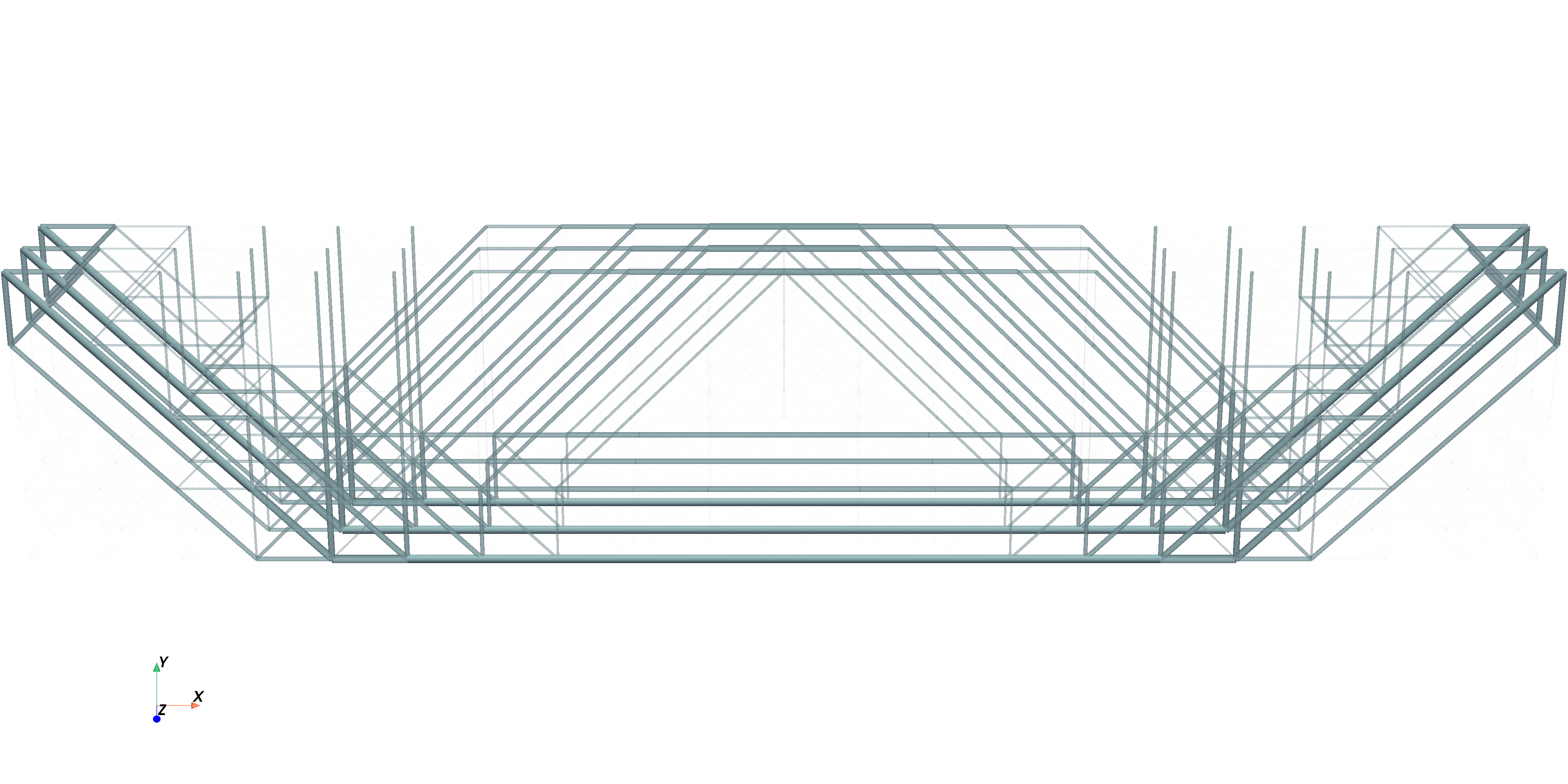
Baratta, I. A., Dean, J. P., Dokken, J. S., Habera, M., Hale, J. S., Richardson, C. N., Rognes, M. E., Scroggs, M. W., Sime, N., & Wells, G. N. (2023). DOLFINx: The next generation FEniCS problem solving environment. Zenodo. 10.5281/zenodo.10447666
Bleyer, J. (2024). Numerical tours of Computational Mechanics with FEniCSx (v0.2) [Computer software]. Zenodo. 10.5281/zenodo.13838486
Christensen, P. W., & Klarbring, A. (2009). Sizing Stiffness Optimization of a Truss. In An Introduction to Structural Optimization (pp. 77–95). Springer Netherlands. 10.1007/978-1-4020-8666-3_5

Obstacle problems

Minimal surfaces in architecture

Structural optimisation

Hyperelasticity in spectral formulation