This demo solves the classic industrial optimisation problem of a General Electric (GE) jet engine bracket under multiple load cases, using the Solid Isotropic Material with Penalisation (SIMP), regularised with a Helmholtz filter.
In particular this demo emphasises
working with a
STEPgeometry,multiple load cases,
multi-step adjoint computations, and
the use of custom optimisation solvers.
The GE jet engine bracket challenge was a competition hosted by GrabCAD in 2013. The goal was to design a bracket that connects an engine to the frame of an aircraft, minimising its weight while remaining in the elastic regime under a set of load cases.
Geometry in the STEP file format is provided on the GrabCAD challenge page. We’ve rotated the
geometry to align the faces with coordinate axes and fragmented the geometry into multiple volumes
to disable the optimisation in the bolt areas. This preprocessing was done in
FreeCAD and is available at the dolfiny github repository
here.
The load cases are defined on the GrabCAD challenge page referenced above, but we include a summary here.
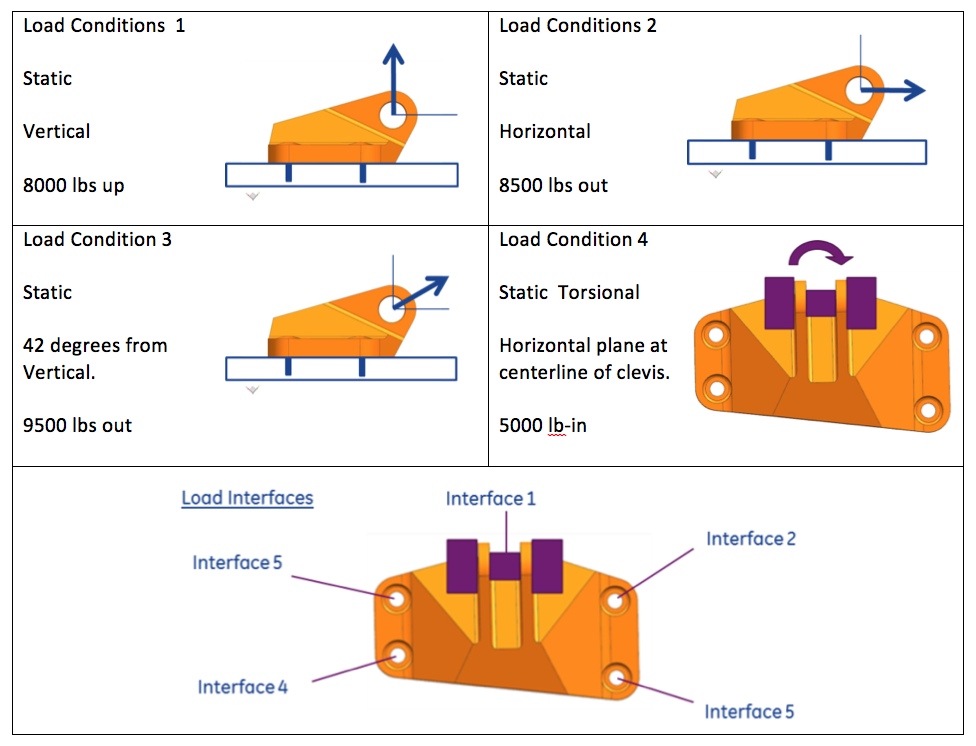
Figure 1:GE jet engine bracket challenge geometry and load cases
(source: https://
We start by importing the necessary modules, reading in the geometry, and generating a mesh with
gmsh. Unfortunately, boolean operations in FreeCAD do not always yield valid geometries, so we
need to call removeAllDuplicates before meshing. Otherwise, this results in disconnected
volumes. Removing duplicates renumbers the faces, so we colour the faces in FreeCAD and extract
the face tags based on the colour.
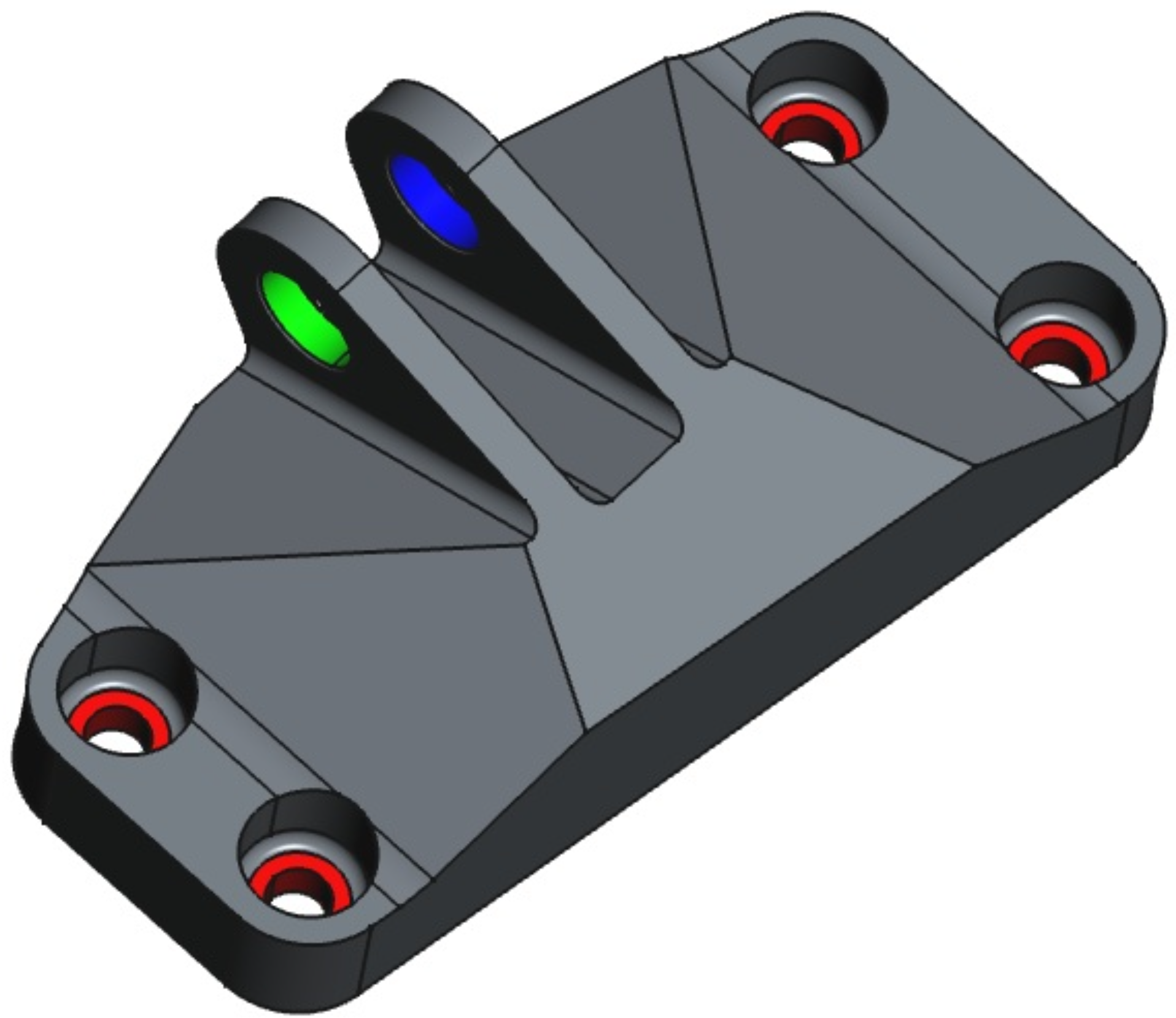
Figure 2:Coloured STEP file pre-processed in FreeCAD, used to identify physical groups.
There are five physical groups:
pin_left(green faces)pin_right(blue faces)bolt_faces(red faces)volume(the main volume for the optimisation)bolts(the bolt volumes where the density is fixed to 1).
The maximum mesh size is set to 3 mm, resulting in approximately 113k tetrahedral elements and 20k
vertices. To resolve the curved geometry, we’ve set Mesh.MeshSizeFromCurvature = 1, which
ensures that the mesh is refined based on the local curvature. More precisely, we have at least 8
elements per . We also use Netgen mesh optimisation to improve the mesh quality.
Additionally, STEP files usually have dimensions in mm, so we ask gmsh to interpret the geometry
in metres by setting Geometry.OCCTargetUnit = M.
from mpi4py import MPI
from petsc4py import PETSc
from petsc4py.PETSc import ScalarType # type: ignore
import dolfinx
import ufl
import gmsh
import numpy as np
import pyvista
import sympy.physics.units as syu
import dolfiny
from dolfiny.units import Quantity
comm = MPI.COMM_WORLD
if comm.rank == 0:
if not gmsh.isInitialized():
gmsh.initialize()
# Convert length units of `CAD` geometry to meters.
gmsh.option.set_string("Geometry.OCCTargetUnit", "M")
gmsh.open("ge_bracket_rotated_nonds.step")
gmsh.model.occ.removeAllDuplicates()
gmsh.model.occ.synchronize()
_, _, surfaces, volumes = (gmsh.model.occ.get_entities(d) for d in range(4))
colors = {
"red": (255, 0, 0, 255),
"green": (0, 255, 0, 255),
"blue": (0, 0, 255, 255),
"yellow": (255, 255, 0, 255),
}
def extract_tags_by_color(a, color):
return list(ai[1] for ai in a if gmsh.model.get_color(*ai) == color)
gmsh.model.addPhysicalGroup(3, [1], name="volume")
gmsh.model.addPhysicalGroup(3, [2, 3, 4, 5], name="bolts")
gmsh.model.addPhysicalGroup(
2, extract_tags_by_color(surfaces, colors["green"]), name="pin_left"
)
gmsh.model.addPhysicalGroup(
2, extract_tags_by_color(surfaces, colors["blue"]), name="pin_right"
)
gmsh.model.addPhysicalGroup(
2, extract_tags_by_color(surfaces, colors["red"]), name="bolt_faces"
)
gmsh.option.setNumber("General.NumThreads", comm.size) # assumes single node execution
gmsh.option.setNumber("Mesh.Algorithm3D", 10) # HXT
gmsh.option.setNumber("Mesh.MeshSizeMax", 3e-3) # in meters
gmsh.option.setNumber("Mesh.MeshSizeFromCurvature", 1)
gmsh.option.setNumber("Mesh.MinimumElementsPerTwoPi", 8)
gmsh.option.setNumber("Mesh.OptimizeNetgen", 1)
gmsh.model.occ.synchronize()
gmsh.model.mesh.generate(3)
model = gmsh.model if comm.rank == 0 else None
mesh_data = dolfinx.io.gmsh.model_to_mesh(gmsh.model, comm, rank=0)
mesh = mesh_data.mesh
pin_left_tag = mesh_data.physical_groups["pin_left"].tag
pin_right_tag = mesh_data.physical_groups["pin_right"].tag
bolt_faces_tags = mesh_data.physical_groups["bolt_faces"].tag
volume_tag = mesh_data.physical_groups["volume"].tag
bolts_tag = mesh_data.physical_groups["bolts"].tagOutput
Info : Reading 'ge_bracket_rotated_nonds.step'...
Info : - Label 'Shapes/BooleanFragments' (3D)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0.447059, 0.47451, 0.501961) (Surface)
Info : - Color (0, 1, 0) (Surface)
Info : - Color (0, 0, 1) (Surface)
Info : - Color (1, 0, 0) (Surface)
Info : - Color (1, 0, 0) (Surface)
Info : - Color (1, 0, 0) (Surface)
Info : - Color (1, 0, 0) (Surface)
Info : - Color (1, 0, 0) (Surface)
Info : - Color (1, 0, 0) (Surface)
Info : - Color (1, 0, 0) (Surface)
Info : - Color (1, 0, 0) (Surface)
Info : - Color (1, 0, 0) (Surface)
Info : - Color (1, 0, 0) (Surface)
Info : - Color (1, 0, 0) (Surface)
Info : - Color (1, 0, 0) (Surface)
Info : - Color (1, 0, 0) (Surface)
Info : - Color (1, 0, 0) (Surface)
Info : Done reading 'ge_bracket_rotated_nonds.step'
Info : Meshing 1D...
Info : [ 0%] Meshing curve 1 (Circle)
Info : [ 10%] Meshing curve 2 (Line)
Info : [ 10%] Meshing curve 3 (Circle)
Info : [ 10%] Meshing curve 4 (Line)
Info : [ 10%] Meshing curve 5 (Circle)
Info : [ 10%] Meshing curve 6 (Line)
Info : [ 10%] Meshing curve 7 (Circle)
Info : [ 10%] Meshing curve 8 (Line)
Info : [ 10%] Meshing curve 9 (Line)
Info : [ 10%] Meshing curve 10 (Line)
Info : [ 10%] Meshing curve 11 (Circle)
Info : [ 10%] Meshing curve 12 (Circle)
Info : [ 10%] Meshing curve 13 (Circle)
Info : [ 10%] Meshing curve 14 (Circle)
Info : [ 10%] Meshing curve 15 (Line)
Info : [ 10%] Meshing curve 16 (Line)
Info : [ 10%] Meshing curve 17 (Circle)
Info : [ 10%] Meshing curve 18 (Line)
Info : [ 20%] Meshing curve 19 (Line)
Info : [ 20%] Meshing curve 20 (Line)
Info : [ 20%] Meshing curve 21 (Line)
Info : [ 20%] Meshing curve 22 (Ellipse)
Info : [ 20%] Meshing curve 23 (Line)
Info : [ 20%] Meshing curve 24 (Line)
Info : [ 20%] Meshing curve 25 (Line)
Info : [ 20%] Meshing curve 26 (Line)
Info : [ 20%] Meshing curve 27 (Line)
Info : [ 20%] Meshing curve 28 (Line)
Info : [ 20%] Meshing curve 29 (Circle)
Info : [ 20%] Meshing curve 30 (Line)
Info : [ 20%] Meshing curve 31 (Line)
Info : [ 20%] Meshing curve 32 (Ellipse)
Info : [ 20%] Meshing curve 33 (Line)
Info : [ 20%] Meshing curve 34 (Line)
Info : [ 20%] Meshing curve 35 (Line)
Info : [ 30%] Meshing curve 36 (Line)
Info : [ 30%] Meshing curve 37 (Ellipse)
Info : [ 30%] Meshing curve 38 (Line)
Info : [ 30%] Meshing curve 39 (Line)
Info : [ 30%] Meshing curve 40 (Line)
Info : [ 30%] Meshing curve 41 (Ellipse)
Info : [ 30%] Meshing curve 42 (Line)
Info : [ 30%] Meshing curve 43 (Line)
Info : [ 30%] Meshing curve 44 (Line)
Info : [ 30%] Meshing curve 45 (Circle)
Info : [ 30%] Meshing curve 46 (Line)
Info : [ 30%] Meshing curve 47 (Circle)
Info : [ 30%] Meshing curve 48 (Line)
Info : [ 30%] Meshing curve 49 (Circle)
Info : [ 30%] Meshing curve 50 (Line)
Info : [ 30%] Meshing curve 51 (Circle)
Info : [ 30%] Meshing curve 52 (Line)
Info : [ 30%] Meshing curve 53 (Circle)
Info : [ 40%] Meshing curve 54 (Line)
Info : [ 40%] Meshing curve 55 (Circle)
Info : [ 40%] Meshing curve 56 (Line)
Info : [ 40%] Meshing curve 57 (Line)
Info : [ 40%] Meshing curve 58 (Circle)
Info : [ 40%] Meshing curve 59 (Line)
Info : [ 40%] Meshing curve 60 (Circle)
Info : [ 40%] Meshing curve 61 (Line)
Info : [ 40%] Meshing curve 62 (Line)
Info : [ 40%] Meshing curve 63 (Ellipse)
Info : [ 40%] Meshing curve 64 (Line)
Info : [ 40%] Meshing curve 65 (Line)
Info : [ 40%] Meshing curve 66 (Line)
Info : [ 40%] Meshing curve 67 (Ellipse)
Info : [ 40%] Meshing curve 68 (Line)
Info : [ 40%] Meshing curve 69 (Ellipse)
Info : [ 40%] Meshing curve 70 (Line)
Info : [ 50%] Meshing curve 71 (Line)
Info : [ 50%] Meshing curve 72 (Line)
Info : [ 50%] Meshing curve 73 (Ellipse)
Info : [ 50%] Meshing curve 74 (Line)
Info : [ 50%] Meshing curve 75 (Line)
Info : [ 50%] Meshing curve 76 (Line)
Info : [ 50%] Meshing curve 77 (Line)
Info : [ 50%] Meshing curve 78 (Line)
Info : [ 50%] Meshing curve 79 (Ellipse)
Info : [ 50%] Meshing curve 80 (Line)
Info : [ 50%] Meshing curve 81 (Line)
Info : [ 50%] Meshing curve 82 (Line)
Info : [ 50%] Meshing curve 83 (Ellipse)
Info : [ 50%] Meshing curve 84 (BSpline)
Info : [ 50%] Meshing curve 85 (Line)
Info : [ 50%] Meshing curve 86 (Circle)
Info : [ 50%] Meshing curve 87 (Line)
Info : [ 50%] Meshing curve 88 (Line)
Info : [ 60%] Meshing curve 89 (Circle)
Info : [ 60%] Meshing curve 90 (Line)
Info : [ 60%] Meshing curve 91 (BSpline)
Info : [ 60%] Meshing curve 92 (Ellipse)
Info : [ 60%] Meshing curve 93 (Line)
Info : [ 60%] Meshing curve 94 (Ellipse)
Info : [ 60%] Meshing curve 95 (Line)
Info : [ 60%] Meshing curve 96 (Line)
Info : [ 60%] Meshing curve 97 (Line)
Info : [ 60%] Meshing curve 98 (Line)
Info : [ 60%] Meshing curve 99 (Line)
Info : [ 60%] Meshing curve 100 (BSpline)
Info : [ 60%] Meshing curve 101 (Line)
Info : [ 60%] Meshing curve 102 (Ellipse)
Info : [ 60%] Meshing curve 103 (Ellipse)
Info : [ 60%] Meshing curve 104 (Line)
Info : [ 60%] Meshing curve 105 (Line)
Info : [ 70%] Meshing curve 106 (Line)
Info : [ 70%] Meshing curve 107 (Ellipse)
Info : [ 70%] Meshing curve 108 (Line)
Info : [ 70%] Meshing curve 109 (Ellipse)
Info : [ 70%] Meshing curve 110 (Line)
Info : [ 70%] Meshing curve 111 (Line)
Info : [ 70%] Meshing curve 112 (BSpline)
Info : [ 70%] Meshing curve 113 (BSpline)
Info : [ 70%] Meshing curve 114 (Circle)
Info : [ 70%] Meshing curve 115 (Circle)
Info : [ 70%] Meshing curve 116 (BSpline)
Info : [ 70%] Meshing curve 117 (Circle)
Info : [ 70%] Meshing curve 118 (Circle)
Info : [ 70%] Meshing curve 119 (BSpline)
Info : [ 70%] Meshing curve 120 (Circle)
Info : [ 70%] Meshing curve 121 (Circle)
Info : [ 70%] Meshing curve 122 (BSpline)
Info : [ 70%] Meshing curve 123 (Circle)
Info : [ 80%] Meshing curve 124 (Circle)
Info : [ 80%] Meshing curve 125 (BSpline)
Info : [ 80%] Meshing curve 126 (BSpline)
Info : [ 80%] Meshing curve 127 (BSpline)
Info : [ 80%] Meshing curve 128 (BSpline)
Info : [ 80%] Meshing curve 129 (Line)
Info : [ 80%] Meshing curve 130 (Circle)
Info : [ 80%] Meshing curve 131 (Circle)
Info : [ 80%] Meshing curve 132 (Circle)
Info : [ 80%] Meshing curve 133 (Circle)
Info : [ 80%] Meshing curve 134 (Line)
Info : [ 80%] Meshing curve 135 (Line)
Info : [ 80%] Meshing curve 136 (Line)
Info : [ 80%] Meshing curve 137 (Line)
Info : [ 80%] Meshing curve 138 (Circle)
Info : [ 80%] Meshing curve 139 (Circle)
Info : [ 80%] Meshing curve 140 (Circle)
Info : [ 90%] Meshing curve 141 (Circle)
Info : [ 90%] Meshing curve 142 (Line)
Info : [ 90%] Meshing curve 143 (BSpline)
Info : [ 90%] Meshing curve 144 (BSpline)
Info : [ 90%] Meshing curve 145 (BSpline)
Info : [ 90%] Meshing curve 146 (BSpline)
Info : [ 90%] Meshing curve 147 (Circle)
Info : [ 90%] Meshing curve 148 (BSpline)
Info : [ 90%] Meshing curve 149 (Circle)
Info : [ 90%] Meshing curve 150 (Circle)
Info : [ 90%] Meshing curve 151 (BSpline)
Info : [ 90%] Meshing curve 152 (Circle)
Info : [ 90%] Meshing curve 153 (BSpline)
Info : [ 90%] Meshing curve 154 (Circle)
Info : [ 90%] Meshing curve 155 (BSpline)
Info : [ 90%] Meshing curve 156 (BSpline)
Info : [ 90%] Meshing curve 157 (BSpline)
Info : [ 90%] Meshing curve 158 (Circle)
Info : [100%] Meshing curve 159 (Circle)
Info : [100%] Meshing curve 160 (Circle)
Info : [100%] Meshing curve 161 (Circle)
Info : [100%] Meshing curve 162 (BSpline)
Info : [100%] Meshing curve 163 (BSpline)
Info : [100%] Meshing curve 164 (Circle)
Info : [100%] Meshing curve 165 (Circle)
Info : [100%] Meshing curve 166 (BSpline)
Info : [100%] Meshing curve 167 (Circle)
Info : [100%] Meshing curve 168 (Circle)
Info : [100%] Meshing curve 169 (BSpline)
Info : [100%] Meshing curve 170 (Circle)
Info : [100%] Meshing curve 171 (Circle)
Info : [100%] Meshing curve 172 (Circle)
Info : [100%] Meshing curve 173 (Circle)
Info : [100%] Meshing curve 174 (BSpline)
Info : [100%] Meshing curve 175 (BSpline)
Info : Done meshing 1D (Wall 0.457042s, CPU 0.435824s)
Info : Meshing 2D...
Info : [ 0%] Meshing surface 1 (Plane, Frontal-Delaunay)
Info : [ 10%] Meshing surface 2 (Cylinder, Frontal-Delaunay)
Info : [ 10%] Meshing surface 3 (Plane, Frontal-Delaunay)
Info : [ 10%] Meshing surface 4 (Plane, Frontal-Delaunay)
Info : [ 10%] Meshing surface 5 (Plane, Frontal-Delaunay)
Info : [ 10%] Meshing surface 6 (Cylinder, Frontal-Delaunay)
Info : [ 10%] Meshing surface 7 (Plane, Frontal-Delaunay)
Info : [ 20%] Meshing surface 8 (Plane, Frontal-Delaunay)
Info : [ 20%] Meshing surface 9 (Cylinder, Frontal-Delaunay)
Info : [ 20%] Meshing surface 10 (Cylinder, Frontal-Delaunay)
Info : [ 20%] Meshing surface 11 (Plane, Frontal-Delaunay)
Info : [ 20%] Meshing surface 12 (Cylinder, Frontal-Delaunay)
Info : [ 20%] Meshing surface 13 (Cylinder, Frontal-Delaunay)
Info : [ 20%] Meshing surface 14 (Cylinder, Frontal-Delaunay)
Info : [ 30%] Meshing surface 15 (Cylinder, Frontal-Delaunay)
Info : [ 30%] Meshing surface 16 (Plane, Frontal-Delaunay)
Info : [ 30%] Meshing surface 17 (Plane, Frontal-Delaunay)
Info : [ 30%] Meshing surface 18 (Plane, Frontal-Delaunay)
Info : [ 30%] Meshing surface 19 (Plane, Frontal-Delaunay)
Info : [ 30%] Meshing surface 20 (Cylinder, Frontal-Delaunay)
Info : [ 30%] Meshing surface 21 (Plane, Frontal-Delaunay)
Info : [ 40%] Meshing surface 22 (Cylinder, Frontal-Delaunay)
Info : [ 40%] Meshing surface 23 (Plane, Frontal-Delaunay)
Info : [ 40%] Meshing surface 24 (Plane, Frontal-Delaunay)
Info : [ 40%] Meshing surface 25 (Cylinder, Frontal-Delaunay)
Info : [ 40%] Meshing surface 26 (Plane, Frontal-Delaunay)
Info : [ 40%] Meshing surface 27 (Cylinder, Frontal-Delaunay)
Info : [ 40%] Meshing surface 28 (Torus, Frontal-Delaunay)
Info : [ 50%] Meshing surface 29 (Torus, Frontal-Delaunay)
Info : [ 50%] Meshing surface 30 (Torus, Frontal-Delaunay)
Info : [ 50%] Meshing surface 31 (Torus, Frontal-Delaunay)
Info : [ 50%] Meshing surface 32 (Cylinder, Frontal-Delaunay)
Info : [ 50%] Meshing surface 33 (Cylinder, Frontal-Delaunay)
Info : [ 50%] Meshing surface 34 (Cylinder, Frontal-Delaunay)
Info : [ 60%] Meshing surface 35 (Cylinder, Frontal-Delaunay)
Info : [ 60%] Meshing surface 36 (Plane, Frontal-Delaunay)
Info : [ 60%] Meshing surface 37 (Cylinder, Frontal-Delaunay)
Info : [ 60%] Meshing surface 38 (Plane, Frontal-Delaunay)
Info : [ 60%] Meshing surface 39 (Cylinder, Frontal-Delaunay)
Info : [ 60%] Meshing surface 40 (Plane, Frontal-Delaunay)
Info : [ 60%] Meshing surface 41 (Cylinder, Frontal-Delaunay)
Info : [ 70%] Meshing surface 42 (Plane, Frontal-Delaunay)
Info : [ 70%] Meshing surface 43 (Cylinder, Frontal-Delaunay)
Info : [ 70%] Meshing surface 44 (Plane, Frontal-Delaunay)
Info : [ 70%] Meshing surface 45 (Cylinder, Frontal-Delaunay)
Info : [ 70%] Meshing surface 46 (Cylinder, Frontal-Delaunay)
Info : [ 70%] Meshing surface 47 (Cylinder, Frontal-Delaunay)
Info : [ 70%] Meshing surface 48 (Cylinder, Frontal-Delaunay)
Info : [ 80%] Meshing surface 49 (Cone, Frontal-Delaunay)
Info : [ 80%] Meshing surface 50 (Cone, Frontal-Delaunay)
Info : [ 80%] Meshing surface 51 (Cone, Frontal-Delaunay)
Info : [ 80%] Meshing surface 52 (Cone, Frontal-Delaunay)
Info : [ 80%] Meshing surface 53 (Cylinder, Frontal-Delaunay)
Info : [ 80%] Meshing surface 54 (Cylinder, Frontal-Delaunay)
Info : [ 80%] Meshing surface 55 (Plane, Frontal-Delaunay)
Info : [ 90%] Meshing surface 56 (Plane, Frontal-Delaunay)
Info : [ 90%] Meshing surface 57 (Cylinder, Frontal-Delaunay)
Info : [ 90%] Meshing surface 58 (Cylinder, Frontal-Delaunay)
Info : [ 90%] Meshing surface 59 (Plane, Frontal-Delaunay)
Info : [ 90%] Meshing surface 60 (Plane, Frontal-Delaunay)
Info : [ 90%] Meshing surface 61 (Cylinder, Frontal-Delaunay)
Info : [ 90%] Meshing surface 62 (Plane, Frontal-Delaunay)
Info : [100%] Meshing surface 63 (Plane, Frontal-Delaunay)
Info : [100%] Meshing surface 64 (Cylinder, Frontal-Delaunay)
Info : [100%] Meshing surface 65 (Plane, Frontal-Delaunay)
Info : [100%] Meshing surface 66 (Plane, Frontal-Delaunay)
Info : [100%] Meshing surface 67 (Cylinder, Frontal-Delaunay)
Info : [100%] Meshing surface 68 (Cylinder, Frontal-Delaunay)
Info : Done meshing 2D (Wall 1.26354s, CPU 0.998044s)
Info : Meshing 3D...
Info : 3D Meshing 5 volumes with 1 connected component
Info : Input mesh hash a5a79c35066d9ba7
Info : Creating an empty mesh with 9120 vertices
Info : Initialization of tet. mesh
Info : Delaunay of 9116 points on 1 threads - mesh.nvert: 4
Info : Recovering 40 missing facet(s)
Info : Recover Delaunay
Info : All volumes of the BRep were found and colorized accordingly
Info : Computing interpolated mesh sizes...
Info : Done computing interpolated mesh sizes
Info : Delaunay of 16858 points on 1 threads - mesh.nvert: 9120
Info : - 14830 points filtered
Info : = 2028 points added
Info : Computing interpolated mesh sizes...
Info : Done computing interpolated mesh sizes
Info : Delaunay of 15468 points on 1 threads - mesh.nvert: 11148
Info : - 11518 points filtered
Info : = 3950 points added
Info : Computing interpolated mesh sizes...
Info : Done computing interpolated mesh sizes
Info : Delaunay of 13468 points on 1 threads - mesh.nvert: 15098
Info : - 9633 points filtered
Info : = 3835 points added
Info : Computing interpolated mesh sizes...
Info : Done computing interpolated mesh sizes
Info : Delaunay of 2721 points on 1 threads - mesh.nvert: 18933
Info : - 1418 points filtered
Info : = 1303 points added
Info : Computing interpolated mesh sizes...
Info : Done computing interpolated mesh sizes
Info : Delaunay of 269 points on 1 threads - mesh.nvert: 20236
Info : - 72 points filtered
Info : = 197 points added
Info : Computing interpolated mesh sizes...
Info : Done computing interpolated mesh sizes
Info : Delaunay of 7 points on 1 threads - mesh.nvert: 20433
Info : - 1 points filtered
Info : = 6 points added
Info : Computing interpolated mesh sizes...
Info : Done computing interpolated mesh sizes
Info : Improving 3584 tet. on 1 thrd (S & ER)
Info : Improving 195 tet. on 1 thrd (S & ER)
Info : Improving 99 tet. on 1 thrd (S & ER)
Info : Improving 90 tet. on 1 thrd (S & ER)
Info : Improving 89 tet. on 1 thrd (S & ER)
Info : Improving 89 tet. on 1 thrd (GSC)
Info : Improving 45 tet. on 1 thrd (S & ER)
Info : Improving 42 tet. on 1 thrd (S & ER)
Info : Improving 41 tet. on 1 thrd (S & ER)
Info : Improving 41 tet. on 1 thrd (GSC)
Info : Improving 35 tet. on 1 thrd (S & ER)
Info : Improving 33 tet. on 1 thrd (S & ER)
Info : Improving 33 tet. on 1 thrd (GSC)
Info : Improving 32 tet. on 1 thrd (S & ER)
Info : Improving 31 tet. on 1 thrd (S & ER)
Info : Improving 31 tet. on 1 thrd (GSC)
Info : Final tet. mesh contains 128266 tetrahedra
Info : Final tet. mesh contains 20439 vertices
Info : tEmptyMesh = 0.189
Info : tVerifyBnd = 0.048
Info : tBndRecovery = 0.239
Info : tConvertMesh = 0.050
Info : tRefine = 0.361
Info : tOptimize = 0.171
Info : Done meshing 3D (Wall 1.61785s, CPU 1.19874s)
Info : 20439 nodes 119194 elements
if comm.size == 1:
grid = pyvista.UnstructuredGrid(*dolfinx.plot.vtk_mesh(mesh))
plotter = pyvista.Plotter(off_screen=True, theme=dolfiny.pyvista.theme)
plotter.add_mesh(
grid, show_edges=True, color="white", line_width=dolfiny.pyvista.pixels // 1000
)
plotter.show_axes()
plotter.camera.elevation = 30
plotter.show()
plotter.close()
plotter.deep_clean()
State problem (linear elasticity)¶
The next step is to define the elasticity problem. We consider a linear isotropic material model, together with the classic SIMP penalisation Bendsøe (1989), which interpolates the Young’s modulus as
where is Young’s modulus of the solid material (associated with the phase ), and is the penalty factor. In this demo we set .
Lower bound on the density, i.e. the density of the void phase is enforced during the optimisation (see below). The lower bound guarantees well-posedness of the elasticity problem. Young’s modulus of the solid phase follows the material specification of Ti-6Al-4V, which is a common aerospace alloy. We’ve taken the approximate value from Ti-6Al-4V. The Poisson’s ratio is set to .
We derive the -th state problem also as a minimisation problem, where the total potential energy is minimised. The total potential energy is defined as
where is the stress tensor, is the small strain tensor, are the applied forces on the boundary parts , and is the displacement field for the -th load condition. The first term is the elastic energy stored in the deformed body, and the second term is the work done by the external forces, which at equilibrium coincides with the compliance.
tdim = mesh.topology.dim
V_u = dolfinx.fem.functionspace(mesh, ("Lagrange", 1, (tdim,)))
V_ρ = dolfinx.fem.functionspace(mesh, ("Discontinuous Lagrange", 0))
V_ρ_f = dolfinx.fem.functionspace(mesh, ("Lagrange", 1))
ρ = dolfinx.fem.Function(V_ρ, name="density")
ρ_f = dolfinx.fem.Function(V_ρ_f, name="density-filtered")
ρ_f.x.array[:] = 1.0
ρ_min = np.float64(1e-3)
penalty = 3
E0 = Quantity(mesh, 110, syu.giga * syu.pascal, "E0") # Ti-6Al-4V
E = ρ_f**penalty * E0
nu = 0.31
def ε(u): # strain
return ufl.sym(ufl.grad(u))
def σ(u): # stress
# Lamé parameters λ and μ
λ = E * nu / ((1 + nu) * (1 - 2 * nu))
μ = E / (2 * (1 + nu))
return λ * ufl.nabla_div(u) * ufl.Identity(len(u)) + 2 * μ * ε(u)
ds = ufl.Measure("ds", domain=mesh, subdomain_data=mesh_data.facet_tags)
dx = ufl.Measure("dx", domain=mesh, subdomain_data=mesh_data.cell_tags)
def compliance(load_condition):
u = load_condition["u"]
return sum(
[ufl.inner(f, u) * m for f, m in zip(load_condition["force"], load_condition["measure"])]
)
def elastic_energy(load_condition):
u = load_condition["u"]
E = 1 / 2 * ufl.inner(σ(u), ε(u)) * dx
E -= compliance(load_condition)
return E
assert isinstance(mesh_data.facet_tags, dolfinx.mesh.MeshTags)
assert isinstance(mesh_data.cell_tags, dolfinx.mesh.MeshTags)
fixed_entities = mesh_data.facet_tags.find(bolt_faces_tags)
fixed_dofs = dolfinx.fem.locate_dofs_topological(V_u, tdim - 1, fixed_entities)
bc_u = dolfinx.fem.dirichletbc(np.zeros(tdim, dtype=ScalarType), fixed_dofs, V_u)
V_ρ_f_bolt_dofs = dolfinx.fem.locate_dofs_topological(
V_ρ_f, tdim, mesh_data.cell_tags.find(mesh_data.physical_groups["bolts"].tag)
)In the challenge specification there are four load cases defined. We need to prepare the
elasticity problem for each load case and store the associated linear problem. This is achieved by
defining a dictionary with the load case name as the key, and the load vectors, measure, the
function to store the solution, and later the LinearProblem.
The first load case is a vertical upward force of on the pin faces. The Neumann boundary force in the weak form is the force per area, so we need to compute the area of the pin faces. In addition, we convert pounds-force to newtons.
The second and third load cases are horizontal and 42 degree angled forces of approximately and , respectively.
The fourth load case is a torsional load, which we model as a couple of forces in opposite directions of on the pin faces. We assume a lever arm of , which we measured as the approximate distance from the centre of the pin holes to the axis around which the torsion acts (midpoint between the pin holes). This couple of forces is the reason why we need to store the force and measure as lists, to allow for multiple Neumann conditions per load case.
Dirichlet boundary conditions are the same for all load cases and correspond to fixing the bolt faces.
We can use convenient unit handling provided by the dolfiny.units.Quantity class to convert the
imperial units to SI units. This will happen automatically, since when we create a Quantity, the
value gets internally converted to base SI units.
pin_area = comm.allreduce(
dolfinx.fem.assemble_scalar(
dolfinx.fem.form(1.0 * ds((pin_left_tag, pin_right_tag), domain=mesh))
)
)
g = Quantity(mesh, 9.81, syu.meter / syu.second**2, "g")
torsion_lever_arm = Quantity(mesh, 0.01, syu.meter, "torsion_lever_arm")
pin_area = Quantity(mesh, pin_area, syu.meter**2, "pin_area")
F1 = Quantity(mesh, 8000, syu.pound, "F1")
F2 = Quantity(mesh, 8500, syu.pound, "F2")
F3 = Quantity(mesh, 9500, syu.pound, "F3")
F4 = Quantity(mesh, 5000, syu.pound * syu.inch, "F4")
load_conditions = {
"vertical_up": {
"force": [F1 * g / pin_area * ufl.as_vector((0, 0, 1))],
"measure": [ds((pin_left_tag, pin_right_tag))],
"u": dolfinx.fem.Function(V_u),
},
"horizontal_out": {
"force": [F2 * g / pin_area * ufl.as_vector((0, -1, 0))],
"measure": [ds((pin_left_tag, pin_right_tag))],
"u": dolfinx.fem.Function(V_u),
},
"42deg_vertical_out": {
"force": [
F3 * g / pin_area * ufl.as_vector((0, -np.sin(np.deg2rad(42)), np.cos(np.deg2rad(42))))
],
"measure": [ds((pin_left_tag, pin_right_tag))],
"u": dolfinx.fem.Function(V_u),
},
"torsion": {
"force": [
F4 / torsion_lever_arm * g / pin_area / 2 * ufl.as_vector((0, -1, 0)),
F4 / torsion_lever_arm * g / pin_area / 2 * ufl.as_vector((0, 1, 0)),
],
"measure": [ds(pin_left_tag), ds(pin_right_tag)],
"u": dolfinx.fem.Function(V_u),
},
}
def build_nullspace(V):
"""Build PETSc nullspace for 3D elasticity
Copied from https://github.com/FEniCS/dolfinx/blob/main/python/demo/demo_elasticity.py
"""
# Create vectors that will span the nullspace
bs = V.dofmap.index_map_bs
length0 = V.dofmap.index_map.size_local
basis = [dolfinx.la.vector(V.dofmap.index_map, bs=bs, dtype=PETSc.ScalarType) for i in range(6)]
b = [b.array for b in basis]
# Get dof indices for each subspace (x, y and z dofs)
dofs = [V.sub(i).dofmap.list.flatten() for i in range(3)]
# Set the three translational rigid body modes
for i in range(3):
b[i][dofs[i]] = 1.0
# Set the three rotational rigid body modes
x = V.tabulate_dof_coordinates()
dofs_block = V.dofmap.list.flatten()
x0, x1, x2 = x[dofs_block, 0], x[dofs_block, 1], x[dofs_block, 2]
b[3][dofs[0]] = -x1
b[3][dofs[1]] = x0
b[4][dofs[0]] = x2
b[4][dofs[2]] = -x0
b[5][dofs[2]] = x1
b[5][dofs[1]] = -x2
dolfinx.la.orthonormalize(basis)
basis_petsc = [
PETSc.Vec().createWithArray(x[: bs * length0], bsize=3, comm=V.mesh.comm) for x in b
]
return PETSc.NullSpace().create(vectors=basis_petsc)
ns = build_nullspace(V_u)
for lc in load_conditions.values():
u_lc = lc["u"]
a = ufl.derivative(
ufl.derivative(elastic_energy(lc), u_lc),
u_lc,
)
L = -ufl.derivative(elastic_energy(lc), u_lc)
L = ufl.replace(L, {u_lc: ufl.as_vector((0, 0, 0))})
elas_prob = dolfinx.fem.petsc.LinearProblem(
a,
L,
bcs=[bc_u],
u=u_lc, # type: ignore
petsc_options=(
{
# Combination of https://github.com/FEniCS/performance-test and https://doi.org/10.1007/s00158-020-02618-z
"ksp_error_if_not_converged": True,
"ksp_type": "cg",
"ksp_rtol": 1.0e-6,
"pc_type": "gamg",
"pc_gamg_type": "agg",
"pc_gamg_agg_nsmooths": 1,
"pc_gamg_threshold": 0.001,
"mg_levels_esteig_ksp_type": "cg",
"mg_levels_ksp_type": "chebyshev",
"mg_levels_ksp_chebyshev_esteig_steps": 50,
"mg_levels_pc_type": "sor",
"pc_gamg_coarse_eq_limit": 1000,
}
),
petsc_options_prefix="elasticity_ksp",
)
elas_prob._A.setNearNullSpace(ns)
lc["linear_problem"] = elas_prob # type: ignore
J_form = dolfinx.fem.form(compliance(lc))
DJ_form = dolfinx.fem.form(-ufl.derivative(elastic_energy(lc), ρ_f))
lc["J_form"] = J_form
lc["DJ_form"] = DJ_formWe can solve one of the load cases to visualise the displacement field. Below is the displacement field for the torsional load case, converted to mm and scaled by a factor of 0.2.
# Solve all load cases
for name in load_conditions.keys():
load_conditions[name]["linear_problem"].solve() # type: ignore
# Plot subplots for all load cases
if comm.size == 1:
plotter = pyvista.Plotter(theme=dolfiny.pyvista.theme, shape=(2, 2))
for i, name in enumerate(load_conditions.keys()):
plotter.subplot(i // 2, i % 2)
u_lc = load_conditions[name]["u"]
grid = pyvista.UnstructuredGrid(*dolfinx.plot.vtk_mesh(u_lc.function_space.mesh)) # type: ignore
assert isinstance(u_lc, dolfinx.fem.Function)
grid.point_data["u"] = u_lc.x.array.reshape((-1, 3)) * 1000 # displacement in mm
grid_warped = grid.warp_by_vector("u", factor=0.2)
plotter.add_mesh(
grid_warped,
show_edges=True,
n_colors=10,
scalar_bar_args={"title": "Displacement [mm]"},
)
plotter.add_text(
name,
font_size=dolfiny.pyvista.pixels // 100,
font="courier",
position="lower_edge",
)
plotter.camera.elevation = -15
plotter.show_axes()
plotter.show()
plotter.close()
plotter.deep_clean()
Filtering¶
We use a Helmholtz filter on the density field, first introduced by Lazarov & Sigmund (2010) in the context of topology optimisation.
In short, for a given density , we solve a (positive definite) Helmholtz equation, yielding the filtered density :
Here is a parameter that controls the filter radius, we choose to be dependent on the maximum cell diameter. In addition to the volumetric term, we also include a boundary term, which acts like a penalisation towards zero Neumann conditions, i.e., it prevents the density from sticking to the boundary, see Wallin et al. (2020). The boundary is here defined as all boundary facets except those with Dirichlet and Neumann conditions applied.
Since the Helmholtz equation is self-adjoint and we need to evaluate its adjoint for the gradient computation later on, we set up the solver to allow for handling of generic right-hand sides. Thus we only have one linear solver and one operator matrix stored for both the forward and adjoint problems.
In addition to the filter, we need to enforce that the density equals 1 in the bolt volumes. This is achieved by setting the corresponding degrees of freedom in the filtered density function to 1 after applying the filter. We also set the unfiltered density to 1 in the bolt volumes when assembling the right-hand side of the filter problem. Setting the density to 1 in the bolt volumes is important from a practical point of view, as the bolts need to be in contact with solid material.
num_cells = mesh.topology.index_map(tdim).size_local
h = mesh.h(tdim, np.arange(0, num_cells))
hmax = comm.allreduce(h.max(), MPI.MAX)
r = 0.5 * hmax
u_f, v_f = ufl.TrialFunction(V_ρ_f), ufl.TestFunction(V_ρ_f)
a_filter = dolfinx.fem.form(
r**2 * ufl.inner(ufl.grad(u_f), ufl.grad(v_f)) * dx
+ u_f * v_f * dx
+ r * ufl.inner(u_f, v_f) * ds
- r * ufl.inner(u_f, v_f) * ds((pin_left_tag, pin_right_tag, bolt_faces_tags))
)
L_filter_ρ = dolfinx.fem.form(ρ * v_f * dx(volume_tag) + 1.0 * v_f * dx(bolts_tag))
s = dolfinx.fem.Function(V_ρ_f, name="s")
L_filter_s = dolfinx.fem.form(s * v_f * dx)
A_filter = dolfinx.fem.petsc.create_matrix(a_filter)
dolfinx.fem.petsc.assemble_matrix(A_filter, a_filter)
A_filter.assemble()
b_filter = dolfinx.fem.petsc.create_vector(V_ρ_f)
opts = PETSc.Options("filter") # type: ignore
opts["ksp_type"] = "cg"
opts["pc_type"] = "jacobi"
opts["ksp_error_if_not_converged"] = True
filter_ksp = PETSc.KSP().create() # type: ignore
filter_ksp.setOptionsPrefix("filter")
filter_ksp.setFromOptions()
filter_ksp.setOperators(A_filter)
def apply_filter(rhs, f) -> None:
"""Compute filtered f from rhs."""
with b_filter.localForm() as b_local:
b_local.set(0.0)
dolfinx.fem.petsc.assemble_vector(b_filter, rhs)
b_filter.ghostUpdate(PETSc.InsertMode.ADD, PETSc.ScatterMode.REVERSE) # type: ignore
b_filter.ghostUpdate(addv=PETSc.InsertMode.INSERT, mode=PETSc.ScatterMode.FORWARD) # type: ignore
filter_ksp.solve(b_filter, f.x.petsc_vec)
f.x.petsc_vec.ghostUpdate(PETSc.InsertMode.INSERT, PETSc.ScatterMode.FORWARD) # type: ignoreOptimisation problem¶
With the state and filtering problems defined, we can define the objective and gradient of the (reduced) optimisation problem.
The objective, to be minimised, is the total compliance for all load cases:
which is the sum of the compliance for each load case. This choice (i.e., to sum the individual compliances) is one of many possible options for how to account for multiple load cases. Other options include minimising the maximum compliance or minimising a weighted sum of compliances. For simplicity, we follow the sum approach, as it is linear (wrt. load cases), and thus the adjoint problems can be solved independently.
We constrain the density to lower and upper bounds:
and constrain the volume of the design to a volume fraction :
The optimisation problem is stated in reduced form in . So and only appear as intermediates. Gradients are then computed through the adjoint formulation. Since the total compliance is the sum of the compliance for each load case, the gradient is also the sum of the gradients for each load case.
The volume fraction in this demo was chosen as 0.3 (30% of the active part of the mesh). Note that the GrabCAD challenge does not specify any value for the volume fraction. The goal is to produce shapes as light as possible under stress limit constraints. This would require a different optimisation setup and is out of the scope of this demo.
mesh_volume = comm.allreduce(
dolfinx.fem.assemble_scalar(dolfinx.fem.form(dolfinx.fem.Constant(mesh, 1.0) * dx(volume_tag)))
)
volume_fraction = ρ / mesh_volume * dx(volume_tag)
max_volume_fraction = 0.3
g = volume_fraction <= max_volume_fraction
ρ.x.array[:] = max_volume_fraction
ρ_f.interpolate(ρ)
apply_filter(L_filter_ρ, ρ_f)
ρ_f.x.array[V_ρ_f_bolt_dofs] = 1.0
@dolfiny.taoproblem.sync_functions([ρ])
def J(_tao, _):
apply_filter(L_filter_ρ, ρ_f)
ρ_f.x.array[V_ρ_f_bolt_dofs] = 1.0
ρ_f.x.array[:] = np.clip(ρ_f.x.array, ρ_min, 1.0)
total = 0.0
for lc_name, lc in load_conditions.items():
lc["linear_problem"].solve()
comp = comm.allreduce(dolfinx.fem.assemble_scalar(lc["J_form"]))
if comm.rank == 0:
print(f"Objective ({lc_name}): {comp:.4g}")
total += comp
return total
Dρ = dolfinx.fem.Function(V_ρ_f)
z = dolfinx.fem.Function(V_ρ_f, name="z")
tmpDG0 = dolfinx.fem.Function(V_ρ)
s_lc_vec = s.x.petsc_vec.copy() # vector to store the gradient contrib. from each load case
@dolfiny.taoproblem.sync_functions([ρ])
def DJ(_tao, _, G):
with s.x.petsc_vec.localForm() as s_local, s_lc_vec.localForm() as s_lc_local:
s_local.set(0.0)
s_lc_local.set(0.0)
for _lc_name, lc in load_conditions.items():
dolfinx.fem.petsc.assemble_vector(s_lc_vec, lc["DJ_form"])
s_lc_vec.ghostUpdate(addv=PETSc.InsertMode.ADD, mode=PETSc.ScatterMode.REVERSE)
s_lc_vec.ghostUpdate(addv=PETSc.InsertMode.INSERT, mode=PETSc.ScatterMode.FORWARD)
with s.x.petsc_vec.localForm() as s_local, s_lc_vec.localForm() as s_lc_local:
s_local += s_lc_local
s_lc_local.set(0.0)
# Apply adjoint to DJ/s -> z.
apply_filter(L_filter_s, z)
z.x.array[V_ρ_f_bolt_dofs] = 0.0
# Interpolate/project z into DG0.
tmpDG0.interpolate(z)
# Copy to G.
tmpDG0.x.petsc_vec.copy(G)
G.ghostUpdate(addv=PETSc.InsertMode.INSERT, mode=PETSc.ScatterMode.FORWARD)
opts = PETSc.Options() # type: ignore
opts["tao_type"] = "python"
opts["tao_monitor"] = ""
opts["tao_max_it"] = (max_it := 50)
opts["tao_python_type"] = "dolfiny.mma.MMA"
opts["tao_mma_move_limit"] = 0.05
opts["tao_mma_subsolver_tao_monitor"] = ""
problem = dolfiny.taoproblem.TAOProblem(
J, [ρ], J=(DJ, ρ.x.petsc_vec.copy()), h=[g], lb=ρ_min, ub=np.float64(1)
)
problem.solve()
with dolfinx.io.XDMFFile(comm, "ge_bracket/result.xdmf", "w") as file:
file.write_mesh(mesh)
for f in (ρ, ρ_f, load_conditions["vertical_up"]["u"]):
file.write_function(f)Output
Objective (vertical_up): 442.5
Objective (horizontal_out): 384.1
Objective (42deg_vertical_out): 259.9
Objective (torsion): 166.4
0 TAO, Function value: 1252.95, Residual: 0.
# TAO 0 (ITERATING)
# sub 0 [ 98k] |x|=9.435e+01 |J|=3.697e+02 (density)
# all |x|=9.435e+01 |J|=3.697e+02 |h|=0.000e+00 |Jh|=0.000e+00 f=1.253e+03
Objective (vertical_up): 442.5
Objective (horizontal_out): 384.1
Objective (42deg_vertical_out): 259.9
Objective (torsion): 166.4
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: 435.277, Residual: 0.11102
1 TAO, Function value: 340.891, Residual: 0.0436347
2 TAO, Function value: 169.777, Residual: 0.00848205
3 TAO, Function value: 161.014, Residual: 0.00207731
4 TAO, Function value: 160.41, Residual: 0.00015278
5 TAO, Function value: 160.407, Residual: 3.35902e-06
6 TAO, Function value: 160.407, Residual: 4.54945e-09
Objective (vertical_up): 309.6
Objective (horizontal_out): 263.6
Objective (42deg_vertical_out): 182.1
Objective (torsion): 107.1
1 TAO, Function value: 862.442, Residual: 202.016
# TAO 1 (ITERATING)
# sub 0 [ 98k] |x|=9.567e+01 |J|=2.020e+02 (density)
# all |x|=9.567e+01 |J|=2.020e+02 |h|=6.106e-16 |Jh|=3.503e-03 f=8.624e+02
Objective (vertical_up): 309.6
Objective (horizontal_out): 263.6
Objective (42deg_vertical_out): 182.1
Objective (torsion): 107.1
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: 4.76841, Residual: 0.0143781
1 TAO, Function value: -1.8367, Residual: 0.0125452
2 TAO, Function value: -18.9616, Residual: 0.00328239
3 TAO, Function value: -19.9333, Residual: 0.000454701
4 TAO, Function value: -19.953, Residual: 1.12412e-05
5 TAO, Function value: -19.953, Residual: 3.2692e-08
Objective (vertical_up): 224.6
Objective (horizontal_out): 191.1
Objective (42deg_vertical_out): 133.5
Objective (torsion): 73.58
2 TAO, Function value: 622.733, Residual: 120.107
# TAO 2 (ITERATING)
# sub 0 [ 98k] |x|=9.995e+01 |J|=1.201e+02 (density)
# all |x|=9.995e+01 |J|=1.201e+02 |h|=3.972e-03 |Jh|=3.503e-03 f=6.227e+02
Objective (vertical_up): 224.6
Objective (horizontal_out): 191.1
Objective (42deg_vertical_out): 133.5
Objective (torsion): 73.58
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -71.9679, Residual: 0.0117423
1 TAO, Function value: -76.2278, Residual: 0.00951393
2 TAO, Function value: -83.4129, Residual: 0.00151011
3 TAO, Function value: -83.5724, Residual: 0.000141509
4 TAO, Function value: -83.5738, Residual: 1.72123e-06
5 TAO, Function value: -83.5738, Residual: 2.81093e-09
Objective (vertical_up): 168.9
Objective (horizontal_out): 144.6
Objective (42deg_vertical_out): 101.6
Objective (torsion): 53.3
3 TAO, Function value: 468.375, Residual: 76.2858
# TAO 3 (ITERATING)
# sub 0 [ 98k] |x|=1.060e+02 |J|=7.629e+01 (density)
# all |x|=1.060e+02 |J|=7.629e+01 |h|=3.926e-03 |Jh|=3.503e-03 f=4.684e+02
Objective (vertical_up): 168.9
Objective (horizontal_out): 144.6
Objective (42deg_vertical_out): 101.6
Objective (torsion): 53.3
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -95.0779, Residual: 0.0105709
1 TAO, Function value: -98.3986, Residual: 0.00782781
2 TAO, Function value: -102.091, Residual: 0.000865249
3 TAO, Function value: -102.132, Residual: 6.01487e-05
4 TAO, Function value: -102.132, Residual: 4.39145e-07
Objective (vertical_up): 130.7
Objective (horizontal_out): 112.8
Objective (42deg_vertical_out): 79.25
Objective (torsion): 40.25
4 TAO, Function value: 363.017, Residual: 51.043
# TAO 4 (ITERATING)
# sub 0 [ 98k] |x|=1.134e+02 |J|=5.104e+01 (density)
# all |x|=1.134e+02 |J|=5.104e+01 |h|=3.362e-03 |Jh|=3.503e-03 f=3.630e+02
Objective (vertical_up): 130.7
Objective (horizontal_out): 112.8
Objective (42deg_vertical_out): 79.25
Objective (torsion): 40.25
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -94.2321, Residual: 0.0104069
1 TAO, Function value: -97.307, Residual: 0.00689007
2 TAO, Function value: -99.5896, Residual: 0.000416897
3 TAO, Function value: -99.5976, Residual: 1.60776e-05
4 TAO, Function value: -99.5976, Residual: 4.83656e-08
Objective (vertical_up): 103.3
Objective (horizontal_out): 89.54
Objective (42deg_vertical_out): 62.75
Objective (torsion): 31.26
5 TAO, Function value: 286.891, Residual: 35.5339
# TAO 5 (ITERATING)
# sub 0 [ 98k] |x|=1.220e+02 |J|=3.553e+01 (density)
# all |x|=1.220e+02 |J|=3.553e+01 |h|=2.917e-03 |Jh|=3.503e-03 f=2.869e+02
Objective (vertical_up): 103.3
Objective (horizontal_out): 89.54
Objective (42deg_vertical_out): 62.75
Objective (torsion): 31.26
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -85.0316, Residual: 0.0104909
1 TAO, Function value: -85.9177, Residual: 0.00938006
2 TAO, Function value: -89.3731, Residual: 0.000226082
3 TAO, Function value: -89.375, Residual: 2.53004e-06
4 TAO, Function value: -89.375, Residual: 1.47086e-09
Objective (vertical_up): 82.98
Objective (horizontal_out): 71.91
Objective (42deg_vertical_out): 50.22
Objective (torsion): 24.68
6 TAO, Function value: 229.795, Residual: 25.4927
# TAO 6 (ITERATING)
# sub 0 [ 98k] |x|=1.316e+02 |J|=2.549e+01 (density)
# all |x|=1.316e+02 |J|=2.549e+01 |h|=2.548e-03 |Jh|=3.503e-03 f=2.298e+02
Objective (vertical_up): 82.98
Objective (horizontal_out): 71.91
Objective (42deg_vertical_out): 50.22
Objective (torsion): 24.68
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -115.737, Residual: 0.00587166
1 TAO, Function value: -116.01, Residual: 0.00508687
2 TAO, Function value: -116.859, Residual: 0.000245935
3 TAO, Function value: -116.861, Residual: 1.35419e-05
4 TAO, Function value: -116.861, Residual: 3.50309e-08
Objective (vertical_up): 72.2
Objective (horizontal_out): 61.92
Objective (42deg_vertical_out): 43.19
Objective (torsion): 20.23
7 TAO, Function value: 197.539, Residual: 19.3909
# TAO 7 (ITERATING)
# sub 0 [ 98k] |x|=1.368e+02 |J|=1.939e+01 (density)
# all |x|=1.368e+02 |J|=1.939e+01 |h|=2.203e-03 |Jh|=3.503e-03 f=1.975e+02
Objective (vertical_up): 72.2
Objective (horizontal_out): 61.92
Objective (42deg_vertical_out): 43.19
Objective (torsion): 20.23
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -113.975, Residual: 0.000687109
1 TAO, Function value: -113.979, Residual: 0.000600432
2 TAO, Function value: -113.991, Residual: 2.97724e-06
3 TAO, Function value: -113.991, Residual: 9.32053e-09
Objective (vertical_up): 64.16
Objective (horizontal_out): 54.61
Objective (42deg_vertical_out): 37.98
Objective (torsion): 17.03
8 TAO, Function value: 173.782, Residual: 15.3411
# TAO 8 (ITERATING)
# sub 0 [ 98k] |x|=1.416e+02 |J|=1.534e+01 (density)
# all |x|=1.416e+02 |J|=1.534e+01 |h|=1.226e-03 |Jh|=3.503e-03 f=1.738e+02
Objective (vertical_up): 64.16
Objective (horizontal_out): 54.61
Objective (42deg_vertical_out): 37.98
Objective (torsion): 17.03
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -106.743, Residual: 0.0025224
1 TAO, Function value: -106.794, Residual: 0.00221157
2 TAO, Function value: -106.962, Residual: 9.52501e-06
3 TAO, Function value: -106.962, Residual: 1.94992e-08
Objective (vertical_up): 57.67
Objective (horizontal_out): 48.84
Objective (42deg_vertical_out): 33.82
Objective (torsion): 14.63
9 TAO, Function value: 154.954, Residual: 12.5293
# TAO 9 (ITERATING)
# sub 0 [ 98k] |x|=1.466e+02 |J|=1.253e+01 (density)
# all |x|=1.466e+02 |J|=1.253e+01 |h|=1.122e-03 |Jh|=3.503e-03 f=1.550e+02
Objective (vertical_up): 57.67
Objective (horizontal_out): 48.84
Objective (42deg_vertical_out): 33.82
Objective (torsion): 14.63
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -99.7584, Residual: 0.00274941
1 TAO, Function value: -99.8186, Residual: 0.00240583
2 TAO, Function value: -100.015, Residual: 1.29392e-06
3 TAO, Function value: -100.015, Residual: 1.80068e-08
Objective (vertical_up): 52.27
Objective (horizontal_out): 44.15
Objective (42deg_vertical_out): 30.41
Objective (torsion): 12.78
10 TAO, Function value: 139.615, Residual: 10.5073
# TAO 10 (ITERATING)
# sub 0 [ 98k] |x|=1.517e+02 |J|=1.051e+01 (density)
# all |x|=1.517e+02 |J|=1.051e+01 |h|=9.727e-04 |Jh|=3.503e-03 f=1.396e+02
Objective (vertical_up): 52.27
Objective (horizontal_out): 44.15
Objective (42deg_vertical_out): 30.41
Objective (torsion): 12.78
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -93.257, Residual: 0.00272877
1 TAO, Function value: -93.3163, Residual: 0.00238375
2 TAO, Function value: -93.5044, Residual: 3.17274e-05
3 TAO, Function value: -93.5044, Residual: 3.67414e-07
Objective (vertical_up): 47.7
Objective (horizontal_out): 40.27
Objective (42deg_vertical_out): 27.55
Objective (torsion): 11.34
11 TAO, Function value: 126.854, Residual: 9.00354
# TAO 11 (ITERATING)
# sub 0 [ 98k] |x|=1.571e+02 |J|=9.004e+00 (density)
# all |x|=1.571e+02 |J|=9.004e+00 |h|=8.292e-04 |Jh|=3.503e-03 f=1.269e+02
Objective (vertical_up): 47.7
Objective (horizontal_out): 40.27
Objective (42deg_vertical_out): 27.55
Objective (torsion): 11.34
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -87.7537, Residual: 0.00233791
1 TAO, Function value: -87.7973, Residual: 0.00204521
2 TAO, Function value: -87.934, Residual: 8.44613e-05
3 TAO, Function value: -87.9342, Residual: 1.12715e-07
Objective (vertical_up): 43.83
Objective (horizontal_out): 37.03
Objective (42deg_vertical_out): 25.14
Objective (torsion): 10.19
12 TAO, Function value: 116.191, Residual: 7.85909
# TAO 12 (ITERATING)
# sub 0 [ 98k] |x|=1.626e+02 |J|=7.859e+00 (density)
# all |x|=1.626e+02 |J|=7.859e+00 |h|=6.905e-04 |Jh|=3.503e-03 f=1.162e+02
Objective (vertical_up): 43.83
Objective (horizontal_out): 37.03
Objective (42deg_vertical_out): 25.14
Objective (torsion): 10.19
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -83.0576, Residual: 0.00193017
1 TAO, Function value: -83.0873, Residual: 0.00168785
2 TAO, Function value: -83.1792, Residual: 0.000101144
3 TAO, Function value: -83.1795, Residual: 1.77707e-06
4 TAO, Function value: -83.1795, Residual: 5.26262e-09
Objective (vertical_up): 40.53
Objective (horizontal_out): 34.33
Objective (42deg_vertical_out): 23.11
Objective (torsion): 9.277
13 TAO, Function value: 107.246, Residual: 6.97199
# TAO 13 (ITERATING)
# sub 0 [ 98k] |x|=1.681e+02 |J|=6.972e+00 (density)
# all |x|=1.681e+02 |J|=6.972e+00 |h|=5.581e-04 |Jh|=3.503e-03 f=1.072e+02
Objective (vertical_up): 40.53
Objective (horizontal_out): 34.33
Objective (42deg_vertical_out): 23.11
Objective (torsion): 9.277
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -78.8816, Residual: 0.00172992
1 TAO, Function value: -78.9054, Residual: 0.00151115
2 TAO, Function value: -78.9776, Residual: 0.00010934
3 TAO, Function value: -78.978, Residual: 2.26761e-06
4 TAO, Function value: -78.978, Residual: 1.40436e-11
Objective (vertical_up): 37.71
Objective (horizontal_out): 32.06
Objective (42deg_vertical_out): 21.38
Objective (torsion): 8.54
14 TAO, Function value: 99.6963, Residual: 6.27148
# TAO 14 (ITERATING)
# sub 0 [ 98k] |x|=1.735e+02 |J|=6.271e+00 (density)
# all |x|=1.735e+02 |J|=6.271e+00 |h|=4.428e-04 |Jh|=3.503e-03 f=9.970e+01
Objective (vertical_up): 37.71
Objective (horizontal_out): 32.06
Objective (42deg_vertical_out): 21.38
Objective (torsion): 8.54
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -89.8018, Residual: 0.0105076
1 TAO, Function value: -92.7287, Residual: 0.0054274
2 TAO, Function value: -93.473, Residual: 0.00157442
3 TAO, Function value: -93.5395, Residual: 2.48084e-05
4 TAO, Function value: -93.5396, Residual: 3.51735e-08
Objective (vertical_up): 36.95
Objective (horizontal_out): 31.12
Objective (42deg_vertical_out): 20.86
Objective (torsion): 8.466
15 TAO, Function value: 97.3926, Residual: 6.04256
# TAO 15 (ITERATING)
# sub 0 [ 98k] |x|=1.748e+02 |J|=6.043e+00 (density)
# all |x|=1.748e+02 |J|=6.043e+00 |h|=3.522e-04 |Jh|=3.503e-03 f=9.739e+01
Objective (vertical_up): 36.95
Objective (horizontal_out): 31.12
Objective (42deg_vertical_out): 20.86
Objective (torsion): 8.466
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -93.2585, Residual: 0.00197863
1 TAO, Function value: -93.2893, Residual: 0.00168589
2 TAO, Function value: -93.3675, Residual: 0.000121046
3 TAO, Function value: -93.3678, Residual: 1.03121e-05
4 TAO, Function value: -93.3678, Residual: 3.43392e-08
Objective (vertical_up): 36.35
Objective (horizontal_out): 30.47
Objective (42deg_vertical_out): 20.44
Objective (torsion): 8.396
16 TAO, Function value: 95.6522, Residual: 5.88178
# TAO 16 (ITERATING)
# sub 0 [ 98k] |x|=1.759e+02 |J|=5.882e+00 (density)
# all |x|=1.759e+02 |J|=5.882e+00 |h|=1.948e-04 |Jh|=3.503e-03 f=9.565e+01
Objective (vertical_up): 36.35
Objective (horizontal_out): 30.47
Objective (42deg_vertical_out): 20.44
Objective (torsion): 8.396
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -92.4533, Residual: 0.000937891
1 TAO, Function value: -92.4602, Residual: 0.000793874
2 TAO, Function value: -92.4775, Residual: 1.34577e-05
3 TAO, Function value: -92.4775, Residual: 4.58568e-07
Objective (vertical_up): 35.83
Objective (horizontal_out): 29.94
Objective (42deg_vertical_out): 20.09
Objective (torsion): 8.332
17 TAO, Function value: 94.1919, Residual: 5.75345
# TAO 17 (ITERATING)
# sub 0 [ 98k] |x|=1.768e+02 |J|=5.753e+00 (density)
# all |x|=1.768e+02 |J|=5.753e+00 |h|=1.762e-04 |Jh|=3.503e-03 f=9.419e+01
Objective (vertical_up): 35.83
Objective (horizontal_out): 29.94
Objective (42deg_vertical_out): 20.09
Objective (torsion): 8.332
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -91.775, Residual: 0.000508928
1 TAO, Function value: -91.777, Residual: 0.000425162
2 TAO, Function value: -91.7817, Residual: 5.5298e-06
3 TAO, Function value: -91.7817, Residual: 5.56291e-08
Objective (vertical_up): 35.39
Objective (horizontal_out): 29.52
Objective (42deg_vertical_out): 19.8
Objective (torsion): 8.276
18 TAO, Function value: 92.9977, Residual: 5.65224
# TAO 18 (ITERATING)
# sub 0 [ 98k] |x|=1.777e+02 |J|=5.652e+00 (density)
# all |x|=1.777e+02 |J|=5.652e+00 |h|=1.328e-04 |Jh|=3.503e-03 f=9.300e+01
Objective (vertical_up): 35.39
Objective (horizontal_out): 29.52
Objective (42deg_vertical_out): 19.8
Objective (torsion): 8.276
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -91.3344, Residual: 8.42744e-05
1 TAO, Function value: -91.3344, Residual: 6.97876e-05
2 TAO, Function value: -91.3345, Residual: 1.47139e-07
Objective (vertical_up): 35.05
Objective (horizontal_out): 29.23
Objective (42deg_vertical_out): 19.58
Objective (torsion): 8.231
19 TAO, Function value: 92.0912, Residual: 5.578
# TAO 19 (ITERATING)
# sub 0 [ 98k] |x|=1.783e+02 |J|=5.578e+00 (density)
# all |x|=1.783e+02 |J|=5.578e+00 |h|=9.758e-05 |Jh|=3.503e-03 f=9.209e+01
Objective (vertical_up): 35.05
Objective (horizontal_out): 29.23
Objective (42deg_vertical_out): 19.58
Objective (torsion): 8.231
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -90.8742, Residual: 2.48559e-05
1 TAO, Function value: -90.8742, Residual: 2.0434e-05
2 TAO, Function value: -90.8742, Residual: 2.5536e-08
Objective (vertical_up): 34.78
Objective (horizontal_out): 29.01
Objective (42deg_vertical_out): 19.4
Objective (torsion): 8.191
20 TAO, Function value: 91.3736, Residual: 5.5207
# TAO 20 (ITERATING)
# sub 0 [ 98k] |x|=1.788e+02 |J|=5.521e+00 (density)
# all |x|=1.788e+02 |J|=5.521e+00 |h|=7.112e-05 |Jh|=3.503e-03 f=9.137e+01
Objective (vertical_up): 34.78
Objective (horizontal_out): 29.01
Objective (42deg_vertical_out): 19.4
Objective (torsion): 8.191
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -90.406, Residual: 0.000272762
1 TAO, Function value: -90.4066, Residual: 0.000223697
2 TAO, Function value: -90.4078, Residual: 5.82602e-06
3 TAO, Function value: -90.4078, Residual: 1.56079e-07
Objective (vertical_up): 34.55
Objective (horizontal_out): 28.83
Objective (42deg_vertical_out): 19.24
Objective (torsion): 8.154
21 TAO, Function value: 90.7685, Residual: 5.47332
# TAO 21 (ITERATING)
# sub 0 [ 98k] |x|=1.792e+02 |J|=5.473e+00 (density)
# all |x|=1.792e+02 |J|=5.473e+00 |h|=5.537e-05 |Jh|=3.503e-03 f=9.077e+01
Objective (vertical_up): 34.55
Objective (horizontal_out): 28.83
Objective (42deg_vertical_out): 19.24
Objective (torsion): 8.154
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -90.009, Residual: 0.000327921
1 TAO, Function value: -90.0099, Residual: 0.000268955
2 TAO, Function value: -90.0116, Residual: 8.64182e-06
3 TAO, Function value: -90.0116, Residual: 2.67641e-07
Objective (vertical_up): 34.36
Objective (horizontal_out): 28.67
Objective (42deg_vertical_out): 19.1
Objective (torsion): 8.122
22 TAO, Function value: 90.2543, Residual: 5.43367
# TAO 22 (ITERATING)
# sub 0 [ 98k] |x|=1.795e+02 |J|=5.434e+00 (density)
# all |x|=1.795e+02 |J|=5.434e+00 |h|=4.490e-05 |Jh|=3.503e-03 f=9.025e+01
Objective (vertical_up): 34.36
Objective (horizontal_out): 28.67
Objective (42deg_vertical_out): 19.1
Objective (torsion): 8.122
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -89.6317, Residual: 0.000342972
1 TAO, Function value: -89.6326, Residual: 0.00028231
2 TAO, Function value: -89.6346, Residual: 1.68964e-05
3 TAO, Function value: -89.6346, Residual: 8.52739e-07
Objective (vertical_up): 34.2
Objective (horizontal_out): 28.53
Objective (42deg_vertical_out): 18.98
Objective (torsion): 8.092
23 TAO, Function value: 89.805, Residual: 5.39919
# TAO 23 (ITERATING)
# sub 0 [ 98k] |x|=1.798e+02 |J|=5.399e+00 (density)
# all |x|=1.798e+02 |J|=5.399e+00 |h|=3.606e-05 |Jh|=3.503e-03 f=8.981e+01
Objective (vertical_up): 34.2
Objective (horizontal_out): 28.53
Objective (42deg_vertical_out): 18.98
Objective (torsion): 8.092
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -89.2917, Residual: 0.00033669
1 TAO, Function value: -89.2925, Residual: 0.000281012
2 TAO, Function value: -89.2946, Residual: 1.03225e-05
3 TAO, Function value: -89.2946, Residual: 3.37831e-07
Objective (vertical_up): 34.06
Objective (horizontal_out): 28.41
Objective (42deg_vertical_out): 18.88
Objective (torsion): 8.066
24 TAO, Function value: 89.4071, Residual: 5.36883
# TAO 24 (ITERATING)
# sub 0 [ 98k] |x|=1.800e+02 |J|=5.369e+00 (density)
# all |x|=1.800e+02 |J|=5.369e+00 |h|=2.931e-05 |Jh|=3.503e-03 f=8.941e+01
Objective (vertical_up): 34.06
Objective (horizontal_out): 28.41
Objective (42deg_vertical_out): 18.88
Objective (torsion): 8.066
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -88.9757, Residual: 0.000320045
1 TAO, Function value: -88.9765, Residual: 0.000270985
2 TAO, Function value: -88.9785, Residual: 3.39419e-06
3 TAO, Function value: -88.9785, Residual: 1.53271e-08
Objective (vertical_up): 33.94
Objective (horizontal_out): 28.29
Objective (42deg_vertical_out): 18.78
Objective (torsion): 8.042
25 TAO, Function value: 89.0487, Residual: 5.34143
# TAO 25 (ITERATING)
# sub 0 [ 98k] |x|=1.802e+02 |J|=5.341e+00 (density)
# all |x|=1.802e+02 |J|=5.341e+00 |h|=2.232e-05 |Jh|=3.503e-03 f=8.905e+01
Objective (vertical_up): 33.94
Objective (horizontal_out): 28.29
Objective (42deg_vertical_out): 18.78
Objective (torsion): 8.042
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -88.6917, Residual: 0.000301553
1 TAO, Function value: -88.6924, Residual: 0.000258941
2 TAO, Function value: -88.6944, Residual: 3.21507e-06
3 TAO, Function value: -88.6944, Residual: 4.53375e-08
Objective (vertical_up): 33.83
Objective (horizontal_out): 28.19
Objective (42deg_vertical_out): 18.69
Objective (torsion): 8.021
26 TAO, Function value: 88.7315, Residual: 5.31721
# TAO 26 (ITERATING)
# sub 0 [ 98k] |x|=1.803e+02 |J|=5.317e+00 (density)
# all |x|=1.803e+02 |J|=5.317e+00 |h|=1.742e-05 |Jh|=3.503e-03 f=8.873e+01
Objective (vertical_up): 33.83
Objective (horizontal_out): 28.19
Objective (42deg_vertical_out): 18.69
Objective (torsion): 8.021
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -88.4388, Residual: 0.00027908
1 TAO, Function value: -88.4394, Residual: 0.000241655
2 TAO, Function value: -88.4412, Residual: 5.07191e-06
3 TAO, Function value: -88.4412, Residual: 1.20532e-08
Objective (vertical_up): 33.73
Objective (horizontal_out): 28.1
Objective (42deg_vertical_out): 18.62
Objective (torsion): 8.002
27 TAO, Function value: 88.4517, Residual: 5.29597
# TAO 27 (ITERATING)
# sub 0 [ 98k] |x|=1.804e+02 |J|=5.296e+00 (density)
# all |x|=1.804e+02 |J|=5.296e+00 |h|=1.352e-05 |Jh|=3.503e-03 f=8.845e+01
Objective (vertical_up): 33.73
Objective (horizontal_out): 28.1
Objective (42deg_vertical_out): 18.62
Objective (torsion): 8.002
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -88.2161, Residual: 0.000222501
1 TAO, Function value: -88.2165, Residual: 0.000193285
2 TAO, Function value: -88.2177, Residual: 6.56767e-07
Objective (vertical_up): 33.65
Objective (horizontal_out): 28.02
Objective (42deg_vertical_out): 18.55
Objective (torsion): 7.985
28 TAO, Function value: 88.2096, Residual: 5.27759
# TAO 28 (ITERATING)
# sub 0 [ 98k] |x|=1.805e+02 |J|=5.278e+00 (density)
# all |x|=1.805e+02 |J|=5.278e+00 |h|=1.060e-05 |Jh|=3.503e-03 f=8.821e+01
Objective (vertical_up): 33.65
Objective (horizontal_out): 28.02
Objective (42deg_vertical_out): 18.55
Objective (torsion): 7.985
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -88.018, Residual: 0.000169123
1 TAO, Function value: -88.0183, Residual: 0.000147682
2 TAO, Function value: -88.019, Residual: 1.32873e-06
3 TAO, Function value: -88.019, Residual: 1.03129e-09
Objective (vertical_up): 33.58
Objective (horizontal_out): 27.95
Objective (42deg_vertical_out): 18.5
Objective (torsion): 7.971
29 TAO, Function value: 87.9973, Residual: 5.26149
# TAO 29 (ITERATING)
# sub 0 [ 98k] |x|=1.806e+02 |J|=5.261e+00 (density)
# all |x|=1.806e+02 |J|=5.261e+00 |h|=9.382e-06 |Jh|=3.503e-03 f=8.800e+01
Objective (vertical_up): 33.58
Objective (horizontal_out): 27.95
Objective (42deg_vertical_out): 18.5
Objective (torsion): 7.971
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -87.8389, Residual: 0.000165105
1 TAO, Function value: -87.8391, Residual: 0.000143923
2 TAO, Function value: -87.8398, Residual: 5.39644e-06
3 TAO, Function value: -87.8398, Residual: 1.55762e-07
Objective (vertical_up): 33.51
Objective (horizontal_out): 27.89
Objective (42deg_vertical_out): 18.45
Objective (torsion): 7.96
30 TAO, Function value: 87.8104, Residual: 5.24734
# TAO 30 (ITERATING)
# sub 0 [ 98k] |x|=1.806e+02 |J|=5.247e+00 (density)
# all |x|=1.806e+02 |J|=5.247e+00 |h|=7.372e-06 |Jh|=3.503e-03 f=8.781e+01
Objective (vertical_up): 33.51
Objective (horizontal_out): 27.89
Objective (42deg_vertical_out): 18.45
Objective (torsion): 7.96
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -87.6785, Residual: 0.000129444
1 TAO, Function value: -87.6787, Residual: 0.000113531
2 TAO, Function value: -87.6791, Residual: 3.89151e-06
3 TAO, Function value: -87.6791, Residual: 3.96932e-08
Objective (vertical_up): 33.45
Objective (horizontal_out): 27.84
Objective (42deg_vertical_out): 18.4
Objective (torsion): 7.949
31 TAO, Function value: 87.6459, Residual: 5.23493
# TAO 31 (ITERATING)
# sub 0 [ 98k] |x|=1.807e+02 |J|=5.235e+00 (density)
# all |x|=1.807e+02 |J|=5.235e+00 |h|=6.480e-06 |Jh|=3.503e-03 f=8.765e+01
Objective (vertical_up): 33.45
Objective (horizontal_out): 27.84
Objective (42deg_vertical_out): 18.4
Objective (torsion): 7.949
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -87.5309, Residual: 9.33968e-05
1 TAO, Function value: -87.5309, Residual: 8.19039e-05
2 TAO, Function value: -87.5312, Residual: 2.36386e-06
3 TAO, Function value: -87.5312, Residual: 1.54107e-08
Objective (vertical_up): 33.4
Objective (horizontal_out): 27.8
Objective (42deg_vertical_out): 18.37
Objective (torsion): 7.939
32 TAO, Function value: 87.4989, Residual: 5.2239
# TAO 32 (ITERATING)
# sub 0 [ 98k] |x|=1.807e+02 |J|=5.224e+00 (density)
# all |x|=1.807e+02 |J|=5.224e+00 |h|=5.575e-06 |Jh|=3.503e-03 f=8.750e+01
Objective (vertical_up): 33.4
Objective (horizontal_out): 27.8
Objective (42deg_vertical_out): 18.37
Objective (torsion): 7.939
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -87.3969, Residual: 7.26464e-05
1 TAO, Function value: -87.3969, Residual: 6.38648e-05
2 TAO, Function value: -87.397, Residual: 1.55356e-06
3 TAO, Function value: -87.397, Residual: 1.95939e-08
Objective (vertical_up): 33.35
Objective (horizontal_out): 27.76
Objective (42deg_vertical_out): 18.33
Objective (torsion): 7.93
33 TAO, Function value: 87.3659, Residual: 5.21398
# TAO 33 (ITERATING)
# sub 0 [ 98k] |x|=1.807e+02 |J|=5.214e+00 (density)
# all |x|=1.807e+02 |J|=5.214e+00 |h|=4.946e-06 |Jh|=3.503e-03 f=8.737e+01
Objective (vertical_up): 33.35
Objective (horizontal_out): 27.76
Objective (42deg_vertical_out): 18.33
Objective (torsion): 7.93
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -87.2762, Residual: 6.03124e-05
1 TAO, Function value: -87.2763, Residual: 5.30809e-05
2 TAO, Function value: -87.2764, Residual: 1.25633e-06
3 TAO, Function value: -87.2764, Residual: 3.66978e-08
Objective (vertical_up): 33.3
Objective (horizontal_out): 27.72
Objective (42deg_vertical_out): 18.3
Objective (torsion): 7.921
34 TAO, Function value: 87.2459, Residual: 5.20504
# TAO 34 (ITERATING)
# sub 0 [ 98k] |x|=1.807e+02 |J|=5.205e+00 (density)
# all |x|=1.807e+02 |J|=5.205e+00 |h|=4.448e-06 |Jh|=3.503e-03 f=8.725e+01
Objective (vertical_up): 33.3
Objective (horizontal_out): 27.72
Objective (42deg_vertical_out): 18.3
Objective (torsion): 7.921
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -87.1666, Residual: 4.56454e-05
1 TAO, Function value: -87.1667, Residual: 4.03064e-05
2 TAO, Function value: -87.1667, Residual: 9.00898e-07
3 TAO, Function value: -87.1667, Residual: 2.01292e-08
Objective (vertical_up): 33.26
Objective (horizontal_out): 27.69
Objective (42deg_vertical_out): 18.27
Objective (torsion): 7.913
35 TAO, Function value: 87.1373, Residual: 5.19698
# TAO 35 (ITERATING)
# sub 0 [ 98k] |x|=1.807e+02 |J|=5.197e+00 (density)
# all |x|=1.807e+02 |J|=5.197e+00 |h|=4.042e-06 |Jh|=3.503e-03 f=8.714e+01
Objective (vertical_up): 33.26
Objective (horizontal_out): 27.69
Objective (42deg_vertical_out): 18.27
Objective (torsion): 7.913
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -87.0663, Residual: 3.33735e-05
1 TAO, Function value: -87.0663, Residual: 2.96404e-05
2 TAO, Function value: -87.0664, Residual: 2.12369e-07
Objective (vertical_up): 33.22
Objective (horizontal_out): 27.67
Objective (42deg_vertical_out): 18.25
Objective (torsion): 7.906
36 TAO, Function value: 87.0389, Residual: 5.18969
# TAO 36 (ITERATING)
# sub 0 [ 98k] |x|=1.808e+02 |J|=5.190e+00 (density)
# all |x|=1.808e+02 |J|=5.190e+00 |h|=3.692e-06 |Jh|=3.503e-03 f=8.704e+01
Objective (vertical_up): 33.22
Objective (horizontal_out): 27.67
Objective (42deg_vertical_out): 18.25
Objective (torsion): 7.906
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -86.9754, Residual: 3.17353e-05
1 TAO, Function value: -86.9754, Residual: 2.82451e-05
2 TAO, Function value: -86.9754, Residual: 1.47666e-07
Objective (vertical_up): 33.18
Objective (horizontal_out): 27.64
Objective (42deg_vertical_out): 18.22
Objective (torsion): 7.899
37 TAO, Function value: 86.9488, Residual: 5.18305
# TAO 37 (ITERATING)
# sub 0 [ 98k] |x|=1.808e+02 |J|=5.183e+00 (density)
# all |x|=1.808e+02 |J|=5.183e+00 |h|=3.586e-06 |Jh|=3.503e-03 f=8.695e+01
Objective (vertical_up): 33.18
Objective (horizontal_out): 27.64
Objective (42deg_vertical_out): 18.22
Objective (torsion): 7.899
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -86.895, Residual: 3.02396e-05
1 TAO, Function value: -86.895, Residual: 2.69555e-05
2 TAO, Function value: -86.895, Residual: 1.47769e-07
Objective (vertical_up): 33.15
Objective (horizontal_out): 27.62
Objective (42deg_vertical_out): 18.2
Objective (torsion): 7.892
38 TAO, Function value: 86.8689, Residual: 5.17717
# TAO 38 (ITERATING)
# sub 0 [ 98k] |x|=1.808e+02 |J|=5.177e+00 (density)
# all |x|=1.808e+02 |J|=5.177e+00 |h|=2.979e-06 |Jh|=3.503e-03 f=8.687e+01
Objective (vertical_up): 33.15
Objective (horizontal_out): 27.62
Objective (42deg_vertical_out): 18.2
Objective (torsion): 7.892
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -86.8242, Residual: 2.50585e-05
1 TAO, Function value: -86.8242, Residual: 2.23788e-05
2 TAO, Function value: -86.8242, Residual: 1.94028e-07
Objective (vertical_up): 33.12
Objective (horizontal_out): 27.61
Objective (42deg_vertical_out): 18.18
Objective (torsion): 7.887
39 TAO, Function value: 86.7985, Residual: 5.17198
# TAO 39 (ITERATING)
# sub 0 [ 98k] |x|=1.808e+02 |J|=5.172e+00 (density)
# all |x|=1.808e+02 |J|=5.172e+00 |h|=3.020e-06 |Jh|=3.503e-03 f=8.680e+01
Objective (vertical_up): 33.12
Objective (horizontal_out): 27.61
Objective (42deg_vertical_out): 18.18
Objective (torsion): 7.887
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -86.7635, Residual: 6.83408e-07
Objective (vertical_up): 33.1
Objective (horizontal_out): 27.6
Objective (42deg_vertical_out): 18.16
Objective (torsion): 7.883
40 TAO, Function value: 86.7388, Residual: 5.16758
# TAO 40 (ITERATING)
# sub 0 [ 98k] |x|=1.808e+02 |J|=5.168e+00 (density)
# all |x|=1.808e+02 |J|=5.168e+00 |h|=2.801e-06 |Jh|=3.503e-03 f=8.674e+01
Objective (vertical_up): 33.1
Objective (horizontal_out): 27.6
Objective (42deg_vertical_out): 18.16
Objective (torsion): 7.883
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -86.7104, Residual: 6.72932e-06
1 TAO, Function value: -86.7104, Residual: 6.04427e-06
2 TAO, Function value: -86.7104, Residual: 1.97615e-08
Objective (vertical_up): 33.08
Objective (horizontal_out): 27.59
Objective (42deg_vertical_out): 18.15
Objective (torsion): 7.879
41 TAO, Function value: 86.6866, Residual: 5.16376
# TAO 41 (ITERATING)
# sub 0 [ 98k] |x|=1.808e+02 |J|=5.164e+00 (density)
# all |x|=1.808e+02 |J|=5.164e+00 |h|=2.975e-06 |Jh|=3.503e-03 f=8.669e+01
Objective (vertical_up): 33.08
Objective (horizontal_out): 27.59
Objective (42deg_vertical_out): 18.15
Objective (torsion): 7.879
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -86.6642, Residual: 7.49201e-06
1 TAO, Function value: -86.6642, Residual: 4.4979e-06
2 TAO, Function value: -86.6642, Residual: 2.90858e-08
Objective (vertical_up): 33.06
Objective (horizontal_out): 27.58
Objective (42deg_vertical_out): 18.13
Objective (torsion): 7.875
42 TAO, Function value: 86.6427, Residual: 5.16058
# TAO 42 (ITERATING)
# sub 0 [ 98k] |x|=1.808e+02 |J|=5.161e+00 (density)
# all |x|=1.808e+02 |J|=5.161e+00 |h|=2.066e-06 |Jh|=3.503e-03 f=8.664e+01
Objective (vertical_up): 33.06
Objective (horizontal_out): 27.58
Objective (42deg_vertical_out): 18.13
Objective (torsion): 7.875
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -86.6241, Residual: 1.58984e-05
1 TAO, Function value: -86.6241, Residual: 1.42996e-05
2 TAO, Function value: -86.6241, Residual: 1.44371e-07
Objective (vertical_up): 33.04
Objective (horizontal_out): 27.57
Objective (42deg_vertical_out): 18.12
Objective (torsion): 7.872
43 TAO, Function value: 86.6048, Residual: 5.15782
# TAO 43 (ITERATING)
# sub 0 [ 98k] |x|=1.808e+02 |J|=5.158e+00 (density)
# all |x|=1.808e+02 |J|=5.158e+00 |h|=1.793e-06 |Jh|=3.503e-03 f=8.660e+01
Objective (vertical_up): 33.04
Objective (horizontal_out): 27.57
Objective (42deg_vertical_out): 18.12
Objective (torsion): 7.872
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -86.5883, Residual: 1.27062e-05
1 TAO, Function value: -86.5883, Residual: 7.65845e-06
2 TAO, Function value: -86.5883, Residual: 8.98692e-08
Objective (vertical_up): 33.03
Objective (horizontal_out): 27.56
Objective (42deg_vertical_out): 18.11
Objective (torsion): 7.869
44 TAO, Function value: 86.5703, Residual: 5.15533
# TAO 44 (ITERATING)
# sub 0 [ 98k] |x|=1.808e+02 |J|=5.155e+00 (density)
# all |x|=1.808e+02 |J|=5.155e+00 |h|=1.785e-06 |Jh|=3.503e-03 f=8.657e+01
Objective (vertical_up): 33.03
Objective (horizontal_out): 27.56
Objective (42deg_vertical_out): 18.11
Objective (torsion): 7.869
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -86.5555, Residual: 9.26036e-06
1 TAO, Function value: -86.5555, Residual: 5.62215e-06
2 TAO, Function value: -86.5555, Residual: 2.97354e-08
Objective (vertical_up): 33.02
Objective (horizontal_out): 27.56
Objective (42deg_vertical_out): 18.1
Objective (torsion): 7.866
45 TAO, Function value: 86.5381, Residual: 5.15301
# TAO 45 (ITERATING)
# sub 0 [ 98k] |x|=1.808e+02 |J|=5.153e+00 (density)
# all |x|=1.808e+02 |J|=5.153e+00 |h|=1.635e-06 |Jh|=3.503e-03 f=8.654e+01
Objective (vertical_up): 33.02
Objective (horizontal_out): 27.56
Objective (42deg_vertical_out): 18.1
Objective (torsion): 7.866
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -86.5247, Residual: 1.26366e-05
1 TAO, Function value: -86.5248, Residual: 7.69148e-06
2 TAO, Function value: -86.5248, Residual: 4.47935e-08
Objective (vertical_up): 33.01
Objective (horizontal_out): 27.55
Objective (42deg_vertical_out): 18.09
Objective (torsion): 7.863
46 TAO, Function value: 86.5078, Residual: 5.15081
# TAO 46 (ITERATING)
# sub 0 [ 98k] |x|=1.808e+02 |J|=5.151e+00 (density)
# all |x|=1.808e+02 |J|=5.151e+00 |h|=1.485e-06 |Jh|=3.503e-03 f=8.651e+01
Objective (vertical_up): 33.01
Objective (horizontal_out): 27.55
Objective (42deg_vertical_out): 18.09
Objective (torsion): 7.863
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -86.4953, Residual: 1.58723e-05
1 TAO, Function value: -86.4953, Residual: 9.86183e-06
2 TAO, Function value: -86.4953, Residual: 1.42225e-07
Objective (vertical_up): 32.99
Objective (horizontal_out): 27.55
Objective (42deg_vertical_out): 18.08
Objective (torsion): 7.861
47 TAO, Function value: 86.479, Residual: 5.14871
# TAO 47 (ITERATING)
# sub 0 [ 98k] |x|=1.808e+02 |J|=5.149e+00 (density)
# all |x|=1.808e+02 |J|=5.149e+00 |h|=1.429e-06 |Jh|=3.503e-03 f=8.648e+01
Objective (vertical_up): 32.99
Objective (horizontal_out): 27.55
Objective (42deg_vertical_out): 18.08
Objective (torsion): 7.861
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -86.4676, Residual: 1.22125e-05
1 TAO, Function value: -86.4676, Residual: 7.61701e-06
2 TAO, Function value: -86.4676, Residual: 1.33028e-08
Objective (vertical_up): 32.98
Objective (horizontal_out): 27.54
Objective (42deg_vertical_out): 18.07
Objective (torsion): 7.859
48 TAO, Function value: 86.4523, Residual: 5.14676
# TAO 48 (ITERATING)
# sub 0 [ 98k] |x|=1.808e+02 |J|=5.147e+00 (density)
# all |x|=1.808e+02 |J|=5.147e+00 |h|=1.194e-06 |Jh|=3.503e-03 f=8.645e+01
Objective (vertical_up): 32.98
Objective (horizontal_out): 27.54
Objective (42deg_vertical_out): 18.07
Objective (torsion): 7.859
Iteration information for tao_mma_subsolver_ solve.
0 TAO, Function value: -86.4414, Residual: 1.01182e-05
1 TAO, Function value: -86.4414, Residual: 6.33969e-06
2 TAO, Function value: -86.4414, Residual: 4.59052e-08
Objective (vertical_up): 32.97
Objective (horizontal_out): 27.54
Objective (42deg_vertical_out): 18.06
Objective (torsion): 7.858
49 TAO, Function value: 86.4269, Residual: 5.14488
# TAO 49 (ITERATING)
# sub 0 [ 98k] |x|=1.808e+02 |J|=5.145e+00 (density)
# all |x|=1.808e+02 |J|=5.145e+00 |h|=1.275e-06 |Jh|=3.503e-03 f=8.643e+01
Post-processing¶
Once the optimisation is done, we can visualise the results. We use pyvista for the
post-processing. Below is the filtered density field, clipped at 0.5 to visualise the solid
structure.
if comm.size == 1:
grid = pyvista.UnstructuredGrid(*dolfinx.plot.vtk_mesh(ρ_f.function_space.mesh))
grid.point_data["density-filtered"] = ρ_f.x.array
grid_clipped = grid.clip_scalar(scalars="density-filtered", invert=False, value=0.5)
plotter = pyvista.Plotter(
off_screen=True,
theme=dolfiny.pyvista.theme,
shape=(1, 2),
window_size=(dolfiny.pyvista.pixels, dolfiny.pyvista.pixels // 2),
)
plotter.add_mesh(grid_clipped, color="white")
plotter.show_axes()
plotter.camera.elevation = 30
plotter.subplot(0, 1)
plotter.add_mesh(grid_clipped, color="white")
plotter.show_axes()
plotter.view_xz()
plotter.camera.azimuth = 180
plotter.show()
plotter.close()
plotter.deep_clean()
- Bendsøe, M. P. (1989). Optimal shape design as a material distribution problem. Structural Optimization, 1(4), 193–202. 10.1007/bf01650949
- Lazarov, B. S., & Sigmund, O. (2010). Filters in topology optimization based on Helmholtz‐type differential equations. International Journal for Numerical Methods in Engineering, 86(6), 765–781. 10.1002/nme.3072
- Wallin, M., Ivarsson, N., Amir, O., & Tortorelli, D. (2020). Consistent boundary conditions for PDE filter regularization in topology optimization. Structural and Multidisciplinary Optimization, 62(3), 1299–1311. 10.1007/s00158-020-02556-w